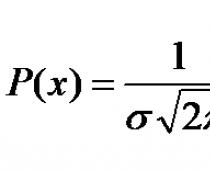Симметрические системы уравнений. §5. Однородные уравнения и системы Работа может использоваться для проведения уроков и докладов по предмету "Математика"

Введение

Симметрия… является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.
Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей. Его широко используют все без исключения направления современной науки.
Об этой закономерности задумывались многие великие люди. Например, Л.Н.Толстой говорил: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?»
Действительно, симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, - всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
Симме́три́я (др.-греч. συμμετρία - «соразмерность»), в широком смысле - неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Цели:

Рассмотреть виды и типы симметрий;

Проанализировать как и где используется симметрия;

Рассмотреть, как симметрия используется в школьном курсе алгебры

Симметрия.
Слово «симметрия» имеет двойственное толкование. В одном смысле симметричное означает нечто весьма пропорциональное, сбалансированное; симметрия показывает тот способ согласования многих частей, с помощью которого они объединяются в целое. Второй смысл этого слова - равновесие. Еще Аристотель говорил о симметрии как о таком состоянии, которое характеризуется соотношением крайностей. Из этого высказывания следует, что Аристотель, пожалуй, был ближе всех к открытию одной из самых фундаментальных закономерностей Природы - закономерности о ее двойственности.
Следует выделить аспекты, без которых симметрия невозможна:
1) объект - носитель симметрии; в роли симметричных объектов могут выступать вещи, процессы, геометрические фигуры, математические выражения, живые организмы и т.д.

2) некоторые признаки - величины, свойства, отношения, процессы, явления - объекта, которые при преобразованиях симметрии остаются неизменными; их называют инвариантными или инвариантами.

3)изменения (объекта), которые оставляют объект тождественным самому себе по инвариантным признакам; такие изменения называются преобразованиями симметрии;

4) свойство объекта превращаться по выделенным признакам в самого себя после соответствующих его изменений.

Таким образом, симметрия выражает сохранение чего-то при каких-то изменениях или сохранение чего-то несмотря на изменение. Симметрия предполагает неизменность не только самого объекта, но и каких-либо его свойств по отношению к преобразованиям, выполненным над объектом. Неизменность тех или иных объектов может наблюдаться по отношению к разнообразным операциям - к поворотам, переносам, взаимной замене частей, отражениям и т.д. В связи с этим выделяют разные типы симметрии.

Асимметрия

Асимметрия - отсутствие или нарушение симметрии.
В архитектуре - симметрия и асимметрия - два противоположных метода закономерной организации пространственной формы. Асимметричные композиции в процессе развития архитектуры возникли как воплощение сложных сочетаний жизненных процессов и условий окружающей среды.

Диссимметрия

Нарушенную, частично расстроенную симметрию мы называем диссимметрией .
Диссимметрия - явление, широко распространенное в живой природе. Она характерна и для человека. Человек диссимметричен, несмотря на то, что очертания его тела имеют плоскость симметрии. Диссимметрия сказывается в
лучшем владении одной из рук, в несимметричном расположении сердца и многих других органов, в строении этих органов.
Диссимметрии человеческого тела подобны и отклонения от точной симметрии в архитектуре. Обычно они вызываются практической необходимостью, тем, что многообразие функций не укладывается в пределы жестких закономерностей симметрии. Иногда такие отклонения дают основу острого эмоционального эффекта.

^ Типы симметрий, встречающиеся в математике и в естественных науках:

Двусторонняя симметрия - симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов Часто существуют небольшие, но закономерные различия во внешнем строении и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.

У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячихУ растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части - листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.

^ Симметрия n-го порядка - симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Zn.

Аксиальная симметрия (радиальная симметрия, лучевая симметрия) -форма симметрии, при которой тело (или фигура) совпадает само с собой при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром симметрии объекта, то есть той точкой, в которой
пересекается бесконечное количество осей двусторонней симметрии. Радиальной симметрией обладают такие геометрические объекты, как круг, шар, цилиндр или конус. Описывается группой SO(2).

^ Сферическая симметрия - симметричность относительно вращений в трёхмерном пространстве на произвольные углы. Описывается группой SO(3). Локальная сферическая симметрия пространства или среды называется также изотропией.

^ Вращательная симметрия - термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства.

^ Симметрия у животных и человека.

Симметрия является жизненно важным признаком, который отражает особенности строения, образа жизни и поведения животного. Симметричность формы необходима рыбе, чтобы плыть; птице, чтобы летать. Так что симметрия в природе существует неспроста: она еще и полезна, или, иначе говоря, целесообразна. В биологии центр симметрии имеют: цветы, медуза, морские звезды и т. д. Наличие форм симметрии прослеживается уже у простейших – одноклеточных (инфузории, амёбы).Тело человека построено по принципу двусторонней симметрии. Мозг разделён на две половины. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого. Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое - левую сторону. Проведенные исследования показали, что симметричное лицо более привлекательно. Также исследователи утверждают, что лицо с идеальными пропорциями является признаком того, что организм его обладателя хорошо подготовлен для борьбы с инфекциями. Обычная простуда, астма и грипп с высокой вероятностью отступают перед людьми, у которых левая сторона в точности похожа на правую. И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина - левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или белой). Но
подобная мода всегда недолговечна. Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.

Симметрия в искусстве

Симметрия в искусстве вообще и в изобразительном в частности берет свое начало в реальной действительности, изобилующей симметрично устроенными формами.
Для симметричной организации композиции характерна уравновешенность ее частей по массам, по тону, цвету и даже по форме. В таких случаях одна часть почти зеркально похожа на вторую. В симметричных композициях чаще всего имеется ярко выраженный центр. Как правило, он совпадает с геометрическим центром картинной плоскости. Если точка схода смещена от центра, одна из частей более загружена по массам или изображение строится по диагонали, все это сообщает динамичность композиции и в какой-то мере нарушает идеальное равновесие.
Правилом симметрии пользовались еще скульпторы Древней Греции. Примером может служить композиция западного фронтона храма Зевса и Олимпии. В основу ее положена борьба лапифов (греков) с кентаврами в присутствии бога Аполлона. Движение постепенно усиливается от краев к центру. Оно достигает предельной выразительности в изображении двух юношей, которые замахнулись на кентавров. Нарастающее движение как бы сразу обрывается на подступах к фигуре Аполлона, спокойно и величественно стоящего в центре фронтона.
Представление об утраченных произведениях знаменитых живописцев V века до н. э. можно составить по античной вазописи и помпейским фрескам, навеянным, как полагают исследователи, произведениями греческих мастеров эпохи классики…
Симметричные композиции наблюдались и у греческих мастеров IV-III веков до н. э. Об этом можно судить по копиям фресок. В помпейских фрес ках главные фигуры находятся в центре пирамидальной композиции, отличающейся симметрией.
К правилам симметрии нередко прибегали художники при изображении торжественных многолюдных собраний, парадов, заседаний в больших залах и т.д.
Большое внимание правилу симметрии уделяли художники раннего Возрождения, о чем свидетельствует монументальная живопись (например, фрески Джотто). В эпоху Высокого Возрождения итальянская композиция достигла зрелости. Например, в картине «Святая Анна с Марией и младенцем Христом» Леонардо да Винчи компонует три фигуры в заостренный кверху треугольник. В правом нижнем углу он дает фигурку агнца, которого держит маленький Христос. Все скомпоновано таким образом, что этот треугольник только угадывается под объемно-пространственной группой фигур.
Симметричной композицией можно назвать и «Тайную вечерю» Леонардо да Винчи. В этой фреске показан драматический момент, когда
Христос сообщил своим ученикам: «Один из вас предаст меня». Психологическая реакция апостолов на эти вещие слова связывает персонажей с композиционным центром, в котором находится фигура Христа. Впечатление целостности от этой центростремительной композиции усиливается еще и тем, что художник показал помещение трапезной в перспективе с точкой схода параллельных линий в середине окна, на фоне которого четко рисуется голова Христа. Таким образом, взор зрителя невольно направляется к центральной фигуре картины.
Среди произведений, демонстрирующих возможности симметрии, можно также назвать «Обручение Марии» Рафаэля, где нашли наиболее полное выражение приемы композиции, характерные для эпохи Возрождения.
Картина В. М. Васнецова «Богатыри» также построена на основе правила симметрии. Центром композиции является фигура Ильи Муромца. Слева и справа, как бы в зеркальном отражении, размещены Алеша Попович и Добрыня Никитич. Фигуры расположены вдоль картинной плоскости спокойно сидящими на конях. Симметричное построение композиции передает состояние относительного покоя. Левая и правая фигуры по массам неодинаковы, что обусловлено идейным замыслом автора. Но обе они менее мощные по сравнению с фигурой Муромца и в целом придают полное равновесие композиции.
Устойчивость композиции вызывает у зрителя чувство уверенности в непобедимости богатырей, защитников земли русской. Мало того, в «Богатырях» передано состояние напряженного покоя на грани перехода в действие. А это значит, что и симметрия несет в себе зародыш динамического движения во времени и пространстве.

Симметрия в алгебре.

Простейшие симметрические выражения относительно корней квадратного уравнения встречаются в теореме Виета. Это позволяет использовать их при решении некоторых задач, относящихся к квадратным уравнениям. Рассмотрим ряд примеров.

Пример 1:

Квадратное уравнение имеет корни и . Не решая этого уравнения, выразим через и суммы , . Выражение симметрическое относительно и . Выразим их через + и , а затем применим теорему Виета.

− 4 1 + 4

−6

27 ≡ 0,

−4 x + 4 y + 27

+(y +6 )

x = 1, x

(x − 1 )

= −6.

y = −6

Заметим, что решение второго уравнения – это ещё не решение системы. Полученные числа необходимо подставить в оставшееся первое уравнение системы. В данном случае после подстановки получаем тождество.

Ответ: (1, – 6).♦

§5. Однородные уравнения и системы
Функция f (x , y )	называется	однородной		k , если
f (tx, ty ) = tk f (x, y ) .	Например, функция f (x , y ) = 4x 3 y − 5xy 3 + x 2 y 2
является однородной степени 4, т. к.		f (tx, ty ) = 4	(tx )3 (ty )− 5 (tx )(ty )3 +
+ (tx ) 2 (ty ) 2 = t 4 (4x 3 y − 5xy 3 + x 2 y 2 ) . Уравнение f (x , y ) = 0, где				f (x, y) –

однородная функция, называется однородным. Оно сводится к уравне-

нию с одним неизвестным, если ввести новую переменную t = x y .

f (x, y) = a,

Система с двумя переменными g (x , y ) = b , где f (x , y ) , g (x , y ) –

однородные функции одной и той же степени, называется однородной. Если ab ≠ 0 , умножим первое уравнение на b , второе – на a и вы-

чтем одно из другого – получим равносильную систему

bf (x, y) − ag(x, y) = 0, g(x, y) = b.

Первое уравнение заменой переменных t =

(или t =

) сведётся к

уравнению с одним неизвестным.

Если a = 0

(b = 0) , то уравнение f (x , y ) = 0 (g (x , y ) = 0) заменой

переменных t =

(или t =

) сведётся к уравнению с одним неизвест-

− xy + y

21 ,

Пример 20. (МГУ, 2001, химфак) Решите систему

− 2xy + 15 = 0.

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

− xy + y 2 = 21,

− xy + y 2

y2 − 2 xy

−2 xy = −15

2xy = − 15

x ≠ 0, y ≠ 0;

19 ± 11

5x 2 − 19xy + 12y 2 = 0 5

− 19

12 = 0

−2 xy = −15

x = 3 y,

y = ±5.

3 ) ,

(− 3 3; −

3 ) , (4; 5) ,

(− 4; − 5) . ♦

§6. Симметрические системы

f (x, y)

называется

симметрической,

f (x, y) = f (y, x) .

f (x, y ) = a

Система уравнений вида

где f (x , y ) , g (x , y ) – симмет-

g (x, y ) = b ,

рические, называется симметрической системой. Такие системы реша-

ются чаще	всего с помощью введения новых	переменных
x + y = u, xy

x 3 + x 3 y 3 + y 3 = 17,

Пример 21. Решите систему уравнений

x + xy + y = 5 .

♦ Эта алгебраическая (симметрическая) система, обычно она решается заменой x + y = u , xy = v . Заметив, что

x 3 + x 3 y 3 + y 3 = (x + y ) (x 2 − xy + y 2 ) + x 3 y 3 =

= (x + y ) ((x + y) 2 − 3 xy) + x3 y3 = u (u2 − 3 v) + v3 ,

перепишем систему в виде

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

− 3 uv + v

u = 5 − v,

6 = 0

V =5

−5 v

v = 3, u = 2

(в старых переменных)

x + y = 2,

x = 2 − y ,

xy = 3,

y 2 − 2 y + 3 = 0

x + y = 3,

x = 3 − y,

x = 2, y = 1,

y −3 y + 2 = 0

x = 1, y = 2.

xy = 2,

Ответ: (2;1 ) ,

(1; 2) . ♦

Литература

1. С. И. Колесникова «Интенсивный курс подготовки к Единому Государственному экзамену». Москва, Айрис – Пресс;

2. «Решение сложных задач Единого Государственного экзамена» Москва, Айрис – Пресс или «Вако», 2011;

3. Журнал «Потенциал» №№1 –2 за 2005 г – статьи С. И. Колесниковой «Иррациональные уравнения» и «Иррациональные неравенства»;

4. С. И. Колесникова «Иррациональные уравнения», Москва, 2010,

ООО«Азбука»;

5. С. И. Колесникова «Иррациональные неравенства », Москва, 2010, ООО«Азбука»;

6. С. И. Колесникова «Уравнения и неравенства, содержащие модули», Москва, 2010, ООО«Азбука».

Контрольные вопросы

1(2). Найдите наименьшую длину промежутка, который содержит все решения неравенства 5x + 1 ≥ 2(x − 1) .

2(2). Решите неравенство x 3 + 8x 2 − 20x ≤ 2x − 4 (не требуется решать кубическое уравнение, т. к. справа и слева есть множитель x − 2 ).

3(2). Решите неравенство 2 − x ≥ x − 3.

4(2). Найдите наименьшую длину промежутка, которому принадле-

жат все решения неравенства	x2 + 5 x − 84	≤ 0 .
	(x + 13 )(x + 14 )

5(3). Найдите сумму квадратов целочисленных решений неравенства

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

4 − x − 8 + x ≤ x +6 .

6(3). Решите неравенство 5 + x − 8 − x ≤ 3 − x .

7(3). Решите неравенство	− x 3 − x −1		≤ x .
				9 − 4x − (x + 3) )

8(3). Решите неравенство	4 − x −(x + 2 ) )(				≤ 0.
		(x + 1 )(x − 2 )(x − 3 )

9(4). Найдите наименьшую длину промежутка, которому принадле-

жат все решения неравенства
	x + 5	x + 2		144 − x < 0.


	X −2	4 x −5	6x − 6
	X −2	4 x −5	6x − 6

10(2). Найдите наименьшую длину промежутка, который содержит все решения неравенства 8 x − 8 ≤ 32 + 4x − x 2 .

11(4). Найдите сумму квадратов всех целочисленных решений нера-

2(2). Найдите наименьшую длину промежутка, который содержит
	(x − 1 )3 (x + 3 )
все решения неравенства				≤ 0 .
	2x − 1	x − 2	) (x − 1 )

3(2). Решите неравенство

4 (x − 3 ) 4 ≥ 4 (x − 7 ,5 ) 4 .

4(4). Решите неравенство

x2 + 3 x − 4

x 2 − 16

2x 2 + 3x − 20

5(3). Решите неравенство (x 2	X +1 ) 2 −2 x 3 + x 2 + x −3 x 2		≥ 0 .
венства 4 − 2x − 1 ≤ 3.	Задачи
	− 5x + 6 + 9 − 2x − 5	≤ 0 .
1(3). Решите неравенство		≤ 0 .
19x 2 − 4x 3 − 4x + 19

10x 2 − 17x − 6

6(4). Найдите все a , при которых уравнение

4 x −

функция f (x ) = x 2 + 4x +

x 2 −

x − 1

− a принимает только

неотрица-

тельные значения.

8(4). Решите уравнение 4 x − 3

x − 1

5x + 14 − 3

5x + 14 − 1

9(4). Решите уравнение

x 2 − 5 +

x 2 −3 = x +1 +

x + 3 .

24 − x 2

9 2 x

10(3). Решите неравенство

≥ 0 .

x2 − 4 7 x − 10

11(3). Три гонщика стартуют одновременно из одной точки круговой трассы и едут с постоянными скоростями в одном направлении. Первый гонщик впервые догнал второго, делая свой пятый круг, в точке, диаметрально противоположной старту, а через полчаса после этого он вторично, не считая момента старта, догнал третьего гонщика. Второй гонщик впервые догнал третьего через 3 часа после старта. Сколько кругов в час делает первый гонщик, если второй проходит круг не менее, чем за двадцать минут?

Введение Проблема моего проекта заключается в том, что для успешной сдачи ЕГЭ требуется умение решать различные системы уравнений, а в курсе средней школы им отведено недостаточно времени, необходимого познать этот вопрос глубже. Цель работы: подготовиться к успешной сдачи ЕГЭ. Задачи работы: Расширить свои знания в области математики, связанные с понятием «симметрия». Повысить свою математическую культуру, используя понятие «симметрия» при решении систем уравнений, называемых симметрическими, а также других задач математики.

Понятие симметрии. Симме́три́я - (др.-греч. συμμετρία), в широком смысле - неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы. Двусторонняя симметрия означает, что право и лево относительно какой-либо плоскости выглядят одинаково.

Решение задач при помощи симметрии. Задача №1 Двое по очереди кладут одинаковые монеты на круглый стол, причём монеты не должны накрывать друг друга. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре? (Иначе говоря, у какого из игроков есть выигрышная стратегия?)

Способы решения симметрических систем. Симметрические системы можно решать методом замены переменных, в роли которых выступают основные симметрические многочлены. Симметрическая система двух уравнений с двумя неизвестными х и у решается подстановкой u = х + у, v = ху.

Пример №2 3 х 2у – 2ху + 3ху 2 = 78, 2х – 3ху + 2у + 8 = 0 С помощью основных симметрических многочленов система может записана в следующем виде 3uv – 2v = 78, 2u – 3v = -8. Выражая из второго уравнения u = и подставляя его в первое уравнение, получим 9v2– 28v – 156 = 0. Корни этого уравнения v 1 = 6 и v 2 = - позволяют найти соответствующие им значения u1 = 5, u2= - из выражения u = .

Решим теперь следующую совокупность систем Решим теперь следующую совокупность систем х + у = 5, и х + у = - , ху = 6 ху = - . х = 5 – у, и у = -х - , ху = 6 ху = - . х = 5 – у, и у = -х - , у (5 – у) = 6 х (-х -) = - . х = 5 – у, и у = -х - , у 1= 3, у 2 =2 х 1 = , х 2 = - х 1 = 2, х 2 = 3, и х 1 = , х 2 = - у 1= 3, у 2 =2 у 1 = - , у 2= Ответ: (2; 3), (3; 2), (; -), (- ;).

Теоремы, используемые при решении симметрических систем. Теорема 1. (о симметрических многочленах) Любой симметрический многочлен от двух переменных представим в виде функции от двух основных симметрических многочленов Другими словами, для любого симметрического многочлена f (x, y) существует такая функция двух переменных φ (u, v), что

Теорема 2. (о симметрических многочленах) Теорема 2. (о симметрических многочленах) Любой симметрический многочлен от трёх переменных представим в виде функции от трёх основных симметрических многочленов: Другими словами, для любого симметрического многочлена f (x, y) существует такая функция трёх переменных θ (u, v, w), что

Более сложные симметрические системы – системы, содержащие модуль: | x – y | + y2 = 3, | x – 1 | + | y – 1 | = 2. Рассмотрим данную систему отдельно при х < 1 и при х ≥ 1. Если х < 1, то: а) при у < х система принимает вид х – у + у 2 = 3, - х + 1 – у + 1 = 2, или х – у + у 2 = 3, х + у = 0, откуда находим х 1 = 1, у 1 = - 1, х 2 = - 3, у2 = 3. Эти пары чисел не принадлежат к рассматриваемой области;

б) при х ≤ у < 1 система принимает вид б) при х ≤ у < 1 система принимает вид - х + у + у 2 = 3, - х + 1 – у + 1 = 2, или - х + у + у 2 = 3, х + у = 0, откуда находим х 1 = 3, у 1 = - 3; х 2 = - 1, у 2 = 1. Эти пары чисел не принадлежат к рассматриваемой области; в) при у ≥ 1 (тогда у > х) система принимает вид - х + у + у 2 = 3, - х + 1 + у – 1 = 2, или - х + у + у 2 = 3, х – у = - 2, откуда находим х 1 = - 3, у 1 = - 1, х 2 = - 1, у 2 = 1. Вторая пара чисел принадлежит рассматриваемой области, т. е. является решением данной системы.

Если х ≥ 1, то: Если х ≥ 1, то: а) х > у и у < 1 система принимает вид х – у + у 2 = 3, х – 1 – у = 1 = 2, или х – у + у 2= 3, х – у = 2, откуда находим х 1 = 1, у 1 = - 1, х 2 = 4, у 2 = 2. Первая пара чисел принадлежит рассматриваемой области, т. Е. является решением данной системы; б) при х > у и у ≥ 1 система принимает вид х – у + у 2 = 3, х – 1 + у – 1 = 2, или х – у + у 2 = 3, х + у = 4, откуда находим х = 1, у = 3. Эта пара чисел не принадлежит рассматриваемой области;

в) при х ≤ у (тогда у ≥ 1) система принимает вид в) при х ≤ у (тогда у ≥ 1) система принимает вид - х + у + у 2 = 3, х – 1 + у – 1 = 2, или - х + у + у 2 = 3, х + у = 4, откуда находим х 1 = 5 + √8, у 1 = - 1 - √8; х 2 = 5 - √8, у 2 = - 1 + √8. Эти пары чисел не принадлежат рассматриваемой области. Таким образом, х 1 = - 1, у 1 = 1; х 2 = 1, у 2 = - 1. Ответ: (- 1; 1); (1; - 1).

Заключение Математика развивает мышление человека, учит посредством логики находить разные пути решения. Так, научившись решать симметрические системы, я поняла, что использовать их можно не только для выполнения конкретных примеров, но я для решения разного рода задач. Я думаю, что проект может принести пользу не только мне. Для тех, кто так же захочет ознакомиться с этой темой, моя работа будет являться хорошим помощником.

Список используемой литературы: Башмаков М. И., «Алгебра и начала анализа», 2-е издание, Москва, «Просвещение», 1992, 350 стр. Рудченко П. А., Яремчук Ф. П., «Алгебра и элементарные функции», справочник; издание третье, переработанное и дополненное; Киев, Наукова, Думка, 1987, 648 стр. Шарыгин И. Ф., « Математика для школьников старших классов», Москва, издательский дом «Дрофа», 1995, 490 стр. Интернет-ресурсы: http://www.college.ru/

Работа может использоваться для проведения уроков и докладов по предмету "Математика"

Готовые презентации по математике используют в качестве наглядных пособий, которые позволяют учителю или родителю продемонстрировать изучаемую тему из учебника с помощью слайдов и таблиц, показать примеры по решению задач и уравнений, а также проверить знания. В данном разделе сайта можно найти и скачать множество готовых презентаций по математике для учащихся 1,2,3,4,5,6 класса, а также презентации по высшей математике для студентов ВУЗов.

1. Уравнения называются симметрическими уравнениями 3-й степени , если они имеют вид
ах 3 + bx 2 + bх + a = 0 .

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства возвратных уравнений:

а) У любого возвратного уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е. (х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0, первое уравнение и доказывает интересующее нас утверждение.

б) У возвратного уравнения корней, равных нулю, нет.

в) При делении многочлена нечетной степени на (х + 1) частное является снова возвратным многочленом и это доказывается по индукции.

Пример .

х 3 + 2x 2 + 2х + 1 = 0.

Решение.

У исходного уравнения обязательно есть корень х = -1, поэтому разделим х 3 + 2x 2 + 2х + 1 на (х + 1) по схеме Горнера:

.	1	2	2	1
-1	1	2 – 1 = 1	2 – 1 = 1	1 – 1 = 0

х 3 + 2x 2 + 2х + 1 = (х + 1)(x 2 + х + 1) = 0.

Квадратное уравнение x 2 + х + 1 = 0 не имеет корней.

Ответ: -1.

2. Уравнения называются симметрическими уравнениями 4-й степени , если они имеют вид
ах 4 + bx 3 + сх 2 + bх + a = 0.

Алгоритм решения подобных уравнений таков:

а) Разделить обе части исходного уравнения на х 2 . Это действие не приведет к потере корня, ведь х = 0 решением заданного уравнения не является.

б) С помощью группировки привести уравнение к виду:

а(x 2 + 1/x 2) + b(x + 1/x) + c = 0.

в) Ввести новую неизвестную: t = (x + 1/x).

Проделаем преобразования:t 2 = x 2 +2 + 1/x 2 . Если теперь выразить x 2 + 1/x 2 , то t 2 – 2 = x 2 + 1/x 2 .

г) Решить в новых переменных полученное квадратное уравнение:

аt 2 + bt + c – 2a = 0.

д) Сделать обратную подстановку.

Пример.

6х 4 – 5х 3 – 38x 2 – 5х + 6 = 0.

Решение.

6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.

6(х 2 + 1/х 2) – 5(х + 1/х) – 38 = 0.

Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2) = t 2 – 2, имеем:

6t 2 – 5t – 50 = 0.

t = -5/2 или t = 10/3.

Вернемся к переменной х. После обратной замены решим два полученных уравнения:

1) x + 1/x = -5/2;

х 2 + 5/2 х +1 = 0;

х = -2 или х = -1/2.

2) x + 1/x = 10/3;

х 2 – 10/3 х + 1 = 0;

х = 3 или х = 1/3.

Ответ: -2; -1/2; 1/3; 3.

Способы решения некоторых видов уравнений высших степеней

1. Уравнения, которые имеют вид (х + а) n + (х + b) n = c, решаются подстановкой t = x + (a + b)/2. Этот метод называется методом симметризации .

Примером такого уравнения может быть уравнение вида (х + а) 4 + (х + b) 4 = c.

Пример.

(х + 3) 4 + (х + 1) 4 = 272.

Решение.

Делаем подстановку, о которой говорилось выше:

t = x + (3 + 1)/2 = х + 2, после упрощения: х = t – 2.

(t – 2 + 3) 4 + (t – 2 + 1) 4 = 272.

(t + 1) 4 + (t – 1) 4 = 272.

Убрав скобки с помощью формул, получим:

t 4 + 4t 3 + 6t 2 + 4t + 1 + t 4 – 4t 3 + 6t 2 – 4t + 1 = 272.

2t 4 + 12t 2 – 270 = 0.

t 4 + 6t 2 – 135 = 0.

t 2 = 9 или t 2 = -15.

Второе уравнение корней не дает, а вот из первого имеем t = ±3.

После обратной замены получим, что х = -5 или х = 1.

Ответ: -5; 1.

Для решения подобных уравнений часто оказывается эффективным и метод разложения на множители левой части уравнения.

2. Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.

Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной.

Пример.

(х + 1)(х + 2)(x + 3)(x + 4) = 24.

Решение.

Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам:

((х + 1)(x + 4))((х + 2)(x + 3)) = 24,

(х 2 + 5х + 4)(х 2 + 5х + 6) = 24.

Сделав замену х 2 + 5х + 4 = t, имеем уравнение

t(t + 2) = 24, оно является квадратным:

t 2 + 2t – 24 = 0.

t = -6 или t = 4.

После выполнения обратной замены, легко находим корни исходного уравнения.

Ответ: -5; 0.

3. Уравнения вида (х + а)(х + b)(x + c)(x + d) = Ах 2 , где аd = cb.

Метод решения заключается в частичном раскрытии скобок, делении обеих частей на х 2 и решении совокупности квадратных уравнений.

Пример.

(х + 12)(х + 2)(x + 3)(x + 8) = 4х 2 .

Решение.

Перемножив в левой части первые две и последние две скобки получим:

(х 2 + 14х + 24)(х 2 + 11х + 24) = 4х 2 . Делим на х 2 ≠ 0.

(х + 14 + 24/х)(х + 11 + 24/х) = 4. Заменой (х + 24/х) = t приходим к квадратному уравнению:

(t + 14)(t + 11) = 4;

t 2 + 25х + 150 = 0.

t = 10 или t = 15.

Произведя обратную замену х + 24/х = 10 или х + 24/х = 15, находим корни.

Ответ: (-15 ± √129)/2; -4; -6.

4. Решить уравнение (3х + 5) 4 + (х + 6) 3 = 4х 2 + 1.

Решение.

Данное уравнение сразу трудно классифицировать и выбрать метод решения. Поэтому сначала преобразуем, используя разность квадратов и разность кубов:

((3х + 5) 2 – 4х 2) + ((х + 6) 3 – 1) = 0. Затем, после вынесения общего множителя, придем к простому уравнению:

(х + 5)(х 2 + 18х + 48) = 0.

Ответ: -5; -9 ± √33.

Задача.

Составить многочлен третьей степени, у которого один корень, равный 4, имеет кратность 2 и корень, равный -2.

Решение.

f(x)/((х – 4) 2 (х + 2)) = q(x) или f(x) = (х – 4) 2 (х + 2)q(x).

Умножив первые две скобки, и приведя подобные слагаемые, получим: f(x) = (х 3 – 6x 2 + 32)q(х).

х 3 – 6x 2 + 32 – многочлен третьей степени, следовательно, q(x) – некоторое число из R (т. е. действительное). Пусть q(x) есть единица, тогда f(x) = х 3 – 6x 2 + 32.

Ответ: f(x) = х 3 – 6x 2 + 32.

Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

1. Уравнения называются симметрическими уравнениями 3-й степени , если они имеют вид
ах 3 + bx 2 + bх + a = 0 .

а) У любого возвратного уравнения нечетной степени всегда есть корень, равный -1.

б) У возвратного уравнения корней, равных нулю, нет.

Пример .

х 3 + 2x 2 + 2х + 1 = 0.

Решение.

У исходного уравнения обязательно есть корень х = -1, поэтому разделим х 3 + 2x 2 + 2х + 1 на (х + 1) по схеме Горнера:

.	1	2	2	1
-1	1	2 – 1 = 1	2 – 1 = 1	1 – 1 = 0

х 3 + 2x 2 + 2х + 1 = (х + 1)(x 2 + х + 1) = 0.

Квадратное уравнение x 2 + х + 1 = 0 не имеет корней.

Ответ: -1.

2. Уравнения называются симметрическими уравнениями 4-й степени , если они имеют вид
ах 4 + bx 3 + сх 2 + bх + a = 0.

Алгоритм решения подобных уравнений таков:

б) С помощью группировки привести уравнение к виду:

а(x 2 + 1/x 2) + b(x + 1/x) + c = 0.

в) Ввести новую неизвестную: t = (x + 1/x).

Проделаем преобразования:t 2 = x 2 +2 + 1/x 2 . Если теперь выразить x 2 + 1/x 2 , то t 2 – 2 = x 2 + 1/x 2 .

г) Решить в новых переменных полученное квадратное уравнение:

аt 2 + bt + c – 2a = 0.

д) Сделать обратную подстановку.

Пример.

6х 4 – 5х 3 – 38x 2 – 5х + 6 = 0.

Решение.

6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.

6(х 2 + 1/х 2) – 5(х + 1/х) – 38 = 0.

Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2) = t 2 – 2, имеем:

6t 2 – 5t – 50 = 0.

t = -5/2 или t = 10/3.

Вернемся к переменной х. После обратной замены решим два полученных уравнения:

1) x + 1/x = -5/2;

х 2 + 5/2 х +1 = 0;

х = -2 или х = -1/2.

2) x + 1/x = 10/3;

х 2 – 10/3 х + 1 = 0;

х = 3 или х = 1/3.

Ответ: -2; -1/2; 1/3; 3.

Способы решения некоторых видов уравнений высших степеней

Примером такого уравнения может быть уравнение вида (х + а) 4 + (х + b) 4 = c.

Пример.

(х + 3) 4 + (х + 1) 4 = 272.

Решение.

Делаем подстановку, о которой говорилось выше:

t = x + (3 + 1)/2 = х + 2, после упрощения: х = t – 2.

(t – 2 + 3) 4 + (t – 2 + 1) 4 = 272.

(t + 1) 4 + (t – 1) 4 = 272.

Убрав скобки с помощью формул, получим:

t 4 + 4t 3 + 6t 2 + 4t + 1 + t 4 – 4t 3 + 6t 2 – 4t + 1 = 272.

2t 4 + 12t 2 – 270 = 0.

t 4 + 6t 2 – 135 = 0.

t 2 = 9 или t 2 = -15.

Второе уравнение корней не дает, а вот из первого имеем t = ±3.

После обратной замены получим, что х = -5 или х = 1.

Ответ: -5; 1.

2. Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.

Пример.

(х + 1)(х + 2)(x + 3)(x + 4) = 24.

Решение.

Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам:

((х + 1)(x + 4))((х + 2)(x + 3)) = 24,

(х 2 + 5х + 4)(х 2 + 5х + 6) = 24.

Сделав замену х 2 + 5х + 4 = t, имеем уравнение

t(t + 2) = 24, оно является квадратным:

t 2 + 2t – 24 = 0.

t = -6 или t = 4.

После выполнения обратной замены, легко находим корни исходного уравнения.

Ответ: -5; 0.

3. Уравнения вида (х + а)(х + b)(x + c)(x + d) = Ах 2 , где аd = cb.

Пример.

(х + 12)(х + 2)(x + 3)(x + 8) = 4х 2 .

Решение.

Перемножив в левой части первые две и последние две скобки получим:

(х 2 + 14х + 24)(х 2 + 11х + 24) = 4х 2 . Делим на х 2 ≠ 0.

(х + 14 + 24/х)(х + 11 + 24/х) = 4. Заменой (х + 24/х) = t приходим к квадратному уравнению:

(t + 14)(t + 11) = 4;

t 2 + 25х + 150 = 0.

t = 10 или t = 15.

Произведя обратную замену х + 24/х = 10 или х + 24/х = 15, находим корни.

Ответ: (-15 ± √129)/2; -4; -6.

4. Решить уравнение (3х + 5) 4 + (х + 6) 3 = 4х 2 + 1.

Решение.

((3х + 5) 2 – 4х 2) + ((х + 6) 3 – 1) = 0. Затем, после вынесения общего множителя, придем к простому уравнению:

(х + 5)(х 2 + 18х + 48) = 0.

Ответ: -5; -9 ± √33.

Задача.

Составить многочлен третьей степени, у которого один корень, равный 4, имеет кратность 2 и корень, равный -2.

Решение.

f(x)/((х – 4) 2 (х + 2)) = q(x) или f(x) = (х – 4) 2 (х + 2)q(x).

Умножив первые две скобки, и приведя подобные слагаемые, получим: f(x) = (х 3 – 6x 2 + 32)q(х).

Ответ: f(x) = х 3 – 6x 2 + 32.

Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Total: 0
Вконтакте0
Google+0
ОК0
Facebook0