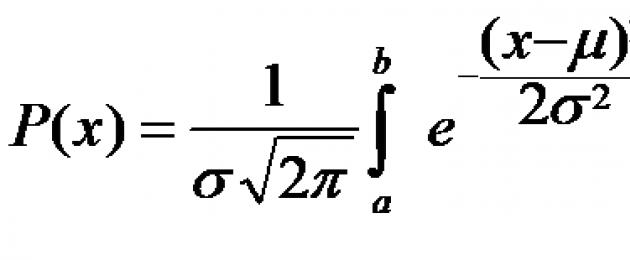Итак, мы приходим к задаче: как найти вероятность, что при следующем испытании случайная величина попадет в наперед заданный интервал?
Для ответа на этот вопрос, прежде всего надо ввести понятие закона распределения случайной величины.
Закон распределения случайной величины (ЗРСВ) – это способ рассчитать вероятность того, что случайная величина (СВ) примет то или иное значение (для дискретных случайных величин) или попадет в тот или иной интервал (для непрерывных случайных величин) в результате испытания.
Для дискретных СВ это чаще всего таблица. Например, для правильной игральной кости эта таблица будет выглядеть так:
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Выпадение 1, 2, 3, 4, 5, или 6 равновероятно и равно одной шестой.
Для непрерывной случайной величины, ЗРСВ может быть задан или в виде графика или в виде формулы. Наибольшее значение в математической статистике имеет нормальный закон распределения случайной величины или закон Гаусса.
Это связано с тем, что очень многие СВ распределены именно по этому закону, в том числе и в биологии и медицине.
Итак, для вычисления вероятностей нам нужен закон Гаусса. Рассмотрим этот закон.
Поставим задачу более точно. Пусть у нас есть некоторая непрерывная случайная величина Х и мы хотим узнать какова вероятность, что при следующем испытании эта величина примет значение х i , лежащие в маленьком интервале от х до х+dx (здесь dx – дифференциал х). Тогда вероятность P(x i), что при следующем испытании это произойдет, по закону Гаусса будет равна:
Формула (1) позволяет рассчитать вероятность попадания следующего измерения в бесконечно маленький интервал dx. Но на практике нам надо научиться рассчитывать вероятность попадания в реальные интервалы, например в интервал от х=а до х=b. Это можно сделать с помощью формулы (2):

Поскольку интервал (а,b) мы задаем сами, следовательно, для расчета вероятности того, что результат следующего испытания попадет в этот интервал нам надо знать только два числа: μ - математическое ожидание и σ - среднее квадратическое отклонение .
Таким образом, оценка этих двух чисел является одной из основных задач математической статистики.
Итак, чтобы решить главную задачу, которая как мы знаем, состоит в том, чтобы научиться рассчитывать вероятность попадания случайной величины в тот или иной наперед заданный интервал, нам надо научиться рассчитывать эти два числа. Вот здесь нас ожидает неудача, поскольку точно рассчитать эти два числа оказалось невозможным! Оказалось, что для того чтобы точно получить эти два числа, например для случайной величины «рост», надо измерить рост у всех людей в мире! Ясно, что мы этого сделать не можем. Что же нам остается? А остается нам измерить рост у тех людей, до которых мы можем добраться, и по полученным значениям ОЦЕНИТЬ значения μ и σ. Подчеркну: не получить точные значения, а только оценить чему приблизительно они равны. Вот эти оценки, которые называются выборочным арифметическим средним () и оценкой среднеквадратичного отклонения (s) и являются самой первой целью большинства статистических исследований.
В нашем рассмотрении неожиданно появилось слово «выборочная». Попробуем объяснить, что оно значит. Для этого введем следующее определение:
Совокупность объектов, из которой отбирается некоторая часть ее членов для изучения, называется генеральной, а отобранная тем или иным способом часть генеральной совокупности называется выборочной совокупностью или выборкой.
В случае с ростом генеральной совокупностью является рост всех людей, тогда как те люди, у которых мы смогли измерить рост, называются выборкой из этой совокупности. Очевидно, что это определение справедливо для любой случайной величины.
РАСЧЕТ И S.
Расчет этих двух величин очень прост и задается следующими двумя формулами:
 (3)
(3)
 (4)
(4)
Чтобы пояснить формулы (3) и (4), представим себе, что мы измеряли рост у 50 человек. Это значит что n=50. Далее складываем все 50 полученных чисел и полученный результат делим на 50. Получаем значение среднего арифметического. Это все расчеты по формуле (3). Расчеты по формуле (4) несколько сложнее. Сначала от всех полученных в результате измерений 50 чисел отнимаем ранее полученную оценку среднего. Получаем 50 значений разности. Потом все 50 разностей возводим в квадрат, после чего все их складываем. Полученный результат делим на 49 (n-1). Из того что получилось, извлекаем квадратный корень. Расчеты среднего арифметического и оценки среднеквадратичного отклонения закончены.
Теперь, когда мы имеем оценки среднего и среднеквадратичного отклонения нам необходимо вернуться к формуле (2). Действительно, оценки μ и σ у нас есть, интервал (а,b) задаем сами, осталось взять интеграл... Но здесь нас подстерегает новая неприятность! Неопределенный интеграл такого вида не берется в элементарных функциях. На наше счастье мы имеем дело не с неопределенным интегралом, а с определенным интегралом. Как мы помним из предыдущего курса, определенный интеграл есть число и существует достаточно много численных методов получения этого числа с любой наперед заданной точностью. Применив один из этих методов, мы получим число, которое и будет вероятностью попадания следующего измерения случайной величины в интервал (a,b). Изменив границы интервала и проведя аналогичные расчеты мы получим вероятность попадания случайной величины в этот новый интервал и т.д. Задача вроде бы решена. У нас есть методика расчета вероятности попадания случайной величины в любой наперед заданный интервал. Однако проведение таких расчетов не очень удобно, поскольку требует много вычислений. Можно ли облегчить себе жизнь? Ну, первое, что приходит на ум это рассчитать все значения интеграла для интервалов, изменяющихся с определенным (небольшим шагом) и занести их в таблицу. Тогда можно пользоваться этой таблицей и ничего не считать. Но эта таблица будет верна, только для той случайной величины, для которой она рассчитывалась. Получается, что нам надо создавать бесчисленное количество таблиц для всевозможных случайных величин. Ясно, что здесь тоже надо что-то придумать. Человечество придумало, как обойтись одной таблицей для всех случаев. Для этого от нашей случайной величины X (любой, которую мы изучаем) надо перейти к другой случайной величине Z, используя следующее соотношение:

Что же мы получим в результате этой операции? Мы получим новую случайную величину, для которой = 0 и s = 1. Эта случайная величина называется нормированной нормально распределенной случайной величиной Z. Поскольку эту операцию можно провести для ЛЮБОЙ случайной величины, подчиняющейся закону Гаусса, мы можем любую случайную величину свести к случайной величине Z, а, следовательно, для расчета вероятности попадания исходной случайной величины в наперед заданный интервал построить ТОЛЬКО ОДНУ таблицу. Конечно же, такая таблица была давно построена, она приведена в приложении 3 и называется таблицей значений функции распределения нормированной нормально распределенной случайной величины
 .(6).
.(6).
Научимся пользоваться этой таблицей. Например рассмотрим число стоящее на пересечении строки, начинающейся с 0,5 и столбца, помеченного цифрой 5. Это число равно 0,7088. Оно показывает, что при следующем испытании вероятность что случайная величина примет значение МЕНЬШЕ 0,55 равна 0,7088. Обратите внимание, что номер столбца есть сотый знак заданного нами числа. Теперь поставим задачу так. Как пользуясь таблицей найти вероятность попадание в интервал (z 1 ,z 2), ведь это и есть наша основная задача. Если z 2 > z 1 , то искомая вероятность будет равна разности Ф(z 2)–Ф(z 1). Например, найдем вероятность, что при следующем испытании значение нормированной случайной величины попадет в интервал (0,95; 1,54). Сначала найдем Ф(1,54). Для этого найдем в таблице строку, которая начинается с 1,5, потом двигаемся по этой строке до столбца, помеченного цифрой 4. Там стоит значение Ф(1,54) = 0,9382. Аналогичным образом найдем Ф(0,95) = 0,8289. Тогда искомая вероятность будет равна: Р = 0,9382 – 0,8289 = 0,1093.
Для полного решения поставленной задачи осталось ответить только на один вопрос: а что если значения z получатся отрицательные? Ведь в таблице приложения 3 нет отрицательных значений. Ответ на этот вопрос дает следующая формула:
Ф(-z) = 1 – Ф(z) (7).
Из формулы (7) следует: если z получилось отрицательным, то надо найти значение Ф(z) по таблице считая z положительным, а потом найденное значение отнять от единицы, это и будет ответом. Теперь задача нахождения вероятности попадания случайной величины, распределенной по закону Гаусса, в любой наперед заданный интервал решена полностью
Для иллюстрации введенных в рассмотрение понятий разберем следующий пример. Пусть в родильном доме за сутки родилось 20 детей, вес которых с точностью до 0,1 килограмма приведен в таблице 1.
Таблица 1
Вес новорожденных в килограммах
| X | 1,8 | 2,1 | 3,1 | 4,2 | 3,6 | 2,2 | 3,1 | 3,9 | 4,4 | 2,6 |
| 3,3 | 3,8 | 3,3 | 4,8 | 2,8 | 3,6 | 3,4 | 2,8 | 3,7 | 3,2 |
Итак, в формуле (2) a=2, b=3

Задача 2.
Решение первой задачи хотя и важно, но конечно не достаточно для практических целей. Следующей важнейшей задачей статистики является получение ответа на вопрос можно ли считать, что какой-то эффект действительно существует или необходимо признать, что на самом деле эффекта нет, и все, что мы наблюдаем есть игра случая. Под эффектом может подразумеваться все что угодно, например, действительно ли жители Скандинавии выше ростом жителей Африки, действительно ли одно лекарство эффективнее другого, действительно ли физиологические параметры изменяются в процессе адаптации, действительно ли успеваемость в одном классе выше успеваемости в другом и т.д.
Очевидно, что все эти задачи нацелены на сравнение двух выборок. Встает вопрос как это сделать. Допустим, мы измеряли рост 10000 жителей Скандинавии и 10000 жителей Африки. Таким образом, мы имеем два набора по 10000 чисел. Ясно, что просто разглядывая эти числа, мы мало чего добьемся. Возникает потребность описать каждый из наборов небольшим количеством производных от них параметров и уже потом сравнивать не сами числа, входящие в тот или иной набор, а эти вновь полученные параметры, характеризующие каждый из наборов. Поскольку вновь полученные параметры описывают сделанную выборку, они получили название «описательные статистики». Описательные статистики можно разделить на несколько групп. Мы будем рассматривать две из них: меры центральной тенденции и меры рассеивания.
Меры центральной тенденции характеризуют центральное значение, вокруг которого распределены значения случайной величины. К ним относятся средняя арифметическая (введена в рассмотрение в предыдущем разделе) и медиана. Средняя арифметическая хорошо подходит для описания распределений, близких к нормальным. Если же распределение существенно отличается от нормального (например, имеет очень длинные и широкие хвосты), то в этом случае имеет смысл использовать для оценки "центрального" значения медиану.
Медиана распределения какой-либо случайной величины X – это такое число Me, для которого вероятность, что при следующем испытании получиться значение исследуемой случайной величины больше Me равно 1/2. Это означает, что вероятность получить значение меньше или равно Me также равна 1/2. Таким образом, медиана характеризует центр распределения в том смысле, что появление значений больше медианы и меньше медианы равновероятны.
Теперь рассмотрим алгоритм, как по значениям выборки оценить медиану. (Обратите внимание на слово «оценить»).
Первое, что надо сделать, это отранжировать, т.е. расположить по возрастающей все значения выборки. Если мы проделаем эту процедуру с выборкой, представленной в предыдущем разделе, то мы получим следующую таблицу:
| X | 1,8 | 2,1 | 2,2 | 2,6 | 2,8 | 2,8 | 3,1 | 3,1 | 3,2 | 3,3 |
| 3,3 | 3,4 | 3,6 | 3,6 | 3,7 | 3,8 | 3,9 | 4,2 | 4,4 | 4,8 |
Далее необходимо определить четное или нечетное число значений в выборке. Если число значений нечетное, то медиана равна значению, находящемуся в центре выборки, если число значений четное, то медиана равна полусумме значений, стоящих в центре выборки. В нашем случае число значений в выборке равно 20, т.е. четное. На 10-м месте стоит число 3,3, а на 11 месте также стоит число 3,3. Следовательно, медиана равна:  . В нашем случае получилось, что медиана и среднее арифметическое равны, но это не всегда так.
. В нашем случае получилось, что медиана и среднее арифметическое равны, но это не всегда так.
Меры рассеивания характеризуют разброс, с которым случайная величина распределяется вокруг своего центрального значения. К этим мерам относятся дисперсия, среднеквадратичное отклонение (введено в рассмотрение в предыдущем разделе), стандартная ошибка среднего, коэффициент вариации.
Если за центральное значение взять среднее арифметическое, то оценку дисперсии можно вычислить по следующей формуле:
 (8).
(8).
Для нашего случая 
Как видно из сравнения формул (4) и (8) оценка среднеквадратичного отклонения связана с оценкой дисперсии следующим соотношением:
 (9)
(9)
В нашем случае  .
.
Большое значение в медицине при проведении расчетов играет такая мера разброса как стандартная ошибка среднего (m), поскольку результаты проведенных исследований часто представляются в виде: ![]() . Формула для расчета оценки стандартной ошибки среднего задается следующим простым соотношением:
. Формула для расчета оценки стандартной ошибки среднего задается следующим простым соотношением:
 (10)
(10)
Для нашего случая 
Изложенные выше меры рассеивания (дисперсия, среднеквадратичное отклонение, стандартная ошибка среднего) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Например, для выборки, представленной в Таблице 1, дисперсия будет выражаться в кг 2 , а среднеквадратичное отклонение и стандартная ошибка в килограммах. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно. Например, если бы мы измеряли не только вес новорожденных, но и их рост, то используя эти меры разброса нельзя было бы ответить на вопрос где изменчивость больше: в случае веса или в случае роста.
Для сравнения изменчивости двух разноименных выборок удобно пользоваться коэффициентом изменчивости (вариации) признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:
 (11).
(11).
В нашем случае 
Чем большеV , тем более изменчив признак. Значения коэффициента вариации, невыходящие за пределы 10% , принято считать нормальными.
Если V>20% , то выборка некомпактна по заданному признаку.
Теперь, когда мы ввели в рассмотрение описательные статистики, задачу определить есть эффект или нет эффекта можно свести к вопросу различаются ли какие либо описательные статистики одной выборки от другой.
Казалось бы решение вопроса очень простое: посчитай описательные статистики одной и второй выборки и сравни их друг с другом. Однако дело обстоит далеко не так просто. Действительно, если бы мы измеряли вес не 20 новорожденных, а скажем, к примеру, только 19, было бы значение среднего и всех остальных описательных статистик тем же самым? Скорее всего НЕТ! Как говорилось, выше мы же всегда имеем дело с выборкой, а не с генеральной совокупностью, поэтому мы всегда получаем ОЦЕНКИ описательных статистик, а не их истинные значения. Следовательно, для решения поставленной задачи нельзя делать выводы, сравнивая непосредственно сами значения. Как же тогда решить задачу?
На помощь приходит понятие доверительного интервала. Идея доверительных интервалов возникает из вопроса: хорошо, мы не знаем точного значения той или иной описательной статистики, но мы хотя бы можем задать интервал, в котором оно находится? Ответ на этот вопрос таков: да мы можем построить интервал, внутри которого содержится точное значение той или иной описательной статистики с наперед заданной вероятностью. Таким образом, мы можем построить доверительный интервал, в котором точное значение описательной статистики содержится с вероятностью, например, 80% или 90%, или 95% или 99% и т.д.
Рассмотрим построение доверительного интервала для среднего значения. В этом случае получается следующее соотношение:
-mt < μ < +mt (12)
В формуле (12) - среднее арифметическое, μ – математическое ожидание (это и есть «истинное» значение, смотри (2)), m – стандартная ошибка среднего (см. (10)). Остается разобраться, что такое t. Буквой t обычно обозначается значение распределения Стьюдента. Расчет конкретного значения распределения Стьюдента для какого-либо конкретного случая довольно сложная задача, поэтому это распределение уже давно затабулировано и представлено в таблице приложения 4.
Рассмотрим эту таблицу. Для отыскания нужного нам значения надо, прежде всего, ответить для себя на вопрос: с какой вероятность мы собираемся строить доверительный интервал? В приложении 4 приведена таблица, которая позволяет строить доверительные интервалы с вероятностями 0,95, 0,99 и 0,999. Если мы задаемся, к примеру, вероятностью 0,95, значит, мы будем использовать первый столбец таблицы. Для того чтобы найти в этом столбце нужное нам число, надо найти строку, которая начинается с числа равного n-1, где n – число измерений. В нашем случае n=20, значит, мы ищем строку, начинающуюся с 19. На пересечении выбранного столбца и нужной строки и стоит нужное нам значение. В нашем случае это число равно 2,093. Следовательно, доверительный интервал будет () или, после вычислений (2,965; 3,635). Итак, истинное среднее (математическое ожидание) с вероятностью 0,95 лежит ГДЕ-ТО между этими двумя числами. Мы написали слово «где-то», чтобы проиллюстрировать одно из свойств доверительных интервалов: любое значение внутри интервала может оказаться математическим ожиданием с одинаковой вероятностью. Второе свойство состоит в том, что мы строили интервал с вероятностью 0,95, это означает, что с этой вероятностью истинное среднее лежит внутри интервала, но это также означает, что с вероятностью 0,05 его нет в данном интервале. Здесь мы впервые сталкиваемся с фундаментальным свойством любого статистического вывода: всегда есть вероятность, что он не верен. Статистический вывод это расчет вероятности справедливости двух гипотез: нулевой и альтернативной. Нулевая гипотеза всегда говорит «нет». Нет различий в описательных статистиках между двумя выборками, нет связи между двумя выборками и т.д. Очевидно, что альтернативная соответственно говорит «да». Возникает вопрос, когда можно считать нулевую гипотезу опровергнутой и принять альтернативную? Для этого нужно задаться уровнем значимости. Уровень значимости - это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда на самом деле она верна. В медицине принят минимальный уровень значимости 0,05. Что это значит? Если в результате расчетов мы получаем что вероятность справедливости нулевой гипотезы меньше 0,05 мы имеем право ее опровергнуть и принять альтернативную гипотезу, тем самым считать доказанным, что различия (а, следовательно, и эффект) есть.
Теперь у нас есть все необходимые понятия, для решения задачи «есть эффект или нет». Пусть мы имеем группу мужчин из 20 больных гипертонией одинакового возрастного диапазона и одинаковой тяжести заболевания. Пусть, далее они принимают новый препарат для снижения артериального давления. Необходимо ответить на вопрос: действительно ли данный препарат эффективен. Проведено фоновое (до лечения) суточное мониторированние систолического артериального давления и получены среднесуточные значения для каждого из 20 человек. После применения схемы лечения, опять проведено суточное мониторированние систолического артериального давления и также получены среднесуточные значения для каждого больного. В результате получены значения представленные в Таблице 2.
Таблица 2
Среднесуточные значения систолического артериального давления до и после лечения
| Номер больного | Среднесуточное систолическое давление (до лечения), мм.рт.ст. | Среднесуточное систолическое давление (после лечения) мм.рт.ст. | Разность систолического давления до лечения и после лечения, мм.рт.ст. |
| +10 | |||
| +10 | |||
| -2 | |||
| +11 | |||
| +8 | |||
| +1 | |||
| +4 | |||
| +9 | |||
| +8 | |||
| +17 | |||
| +9 | |||
| +17 | |||
| +11 | |||
| +11 | |||
| +27 | |||
| +11 | |||
| +22 | |||
| -1 | |||
| +15 | |||
| +21 | |||
| 177,1 | 166.2 | 11,0 | |
| s | 6,8 | 8,4 | 7,5 |
| m | 1,5 | 1,9 | 1,7 |
| |  |  |
Алгоритм решения задачи с помощью доверительных интервалов.
Таким образом, можно решить Задачу 2 с помощью построения доверительных интервалов. Однако более часто используется другой подход для решения этой задачи. Он построен на вычислении экспериментального значения распределения Стьюдента и сравнения его с табличным.
Для построения этого алгоритма решения задачи 2 надо ввести еще два понятия. Зададимся вопросом можно ли в таблице 2 переставлять экспериментальные данные в столбцах произвольным порядком? Ответ: конечно нет, ведь в таком случае данные, полученные на одном пациенте попадут к другому! Такие выборки называются связанными выборками. В нашем случае они связаны номером пациента. Для таких выборок экспериментальное значение распределения Стьюдента рассчитывается по формуле:
 (13)
(13)
В формуле (13) - среднее арифметическое разности, - среднеквадратичное отклонение для разности, - ошибка среднего для разности. Используя значения в таблице 2, рассчитаем .

Как мы уже знаем, табличное значение () для уровня 0,95 и числа степеней свободы 19 (20-1) равно 2,086, следовательно, в нашем случае  . Следовательно, наблюдаемые различия в артериальном давлении действительно существуют. В настоящий момент мы делаем этот вывод на уровне значимости 0,05. Но теперь, когда мы имеем экспериментальное значение распределения Стьюдента, мы можем его сравнить с табличными значениями для других доверительных вероятностей. Посмотрим, например, чему равно табличное значение распределения Стьюдента для доверительной вероятности 0,99 (уровень значимости 0,01). Как следует из таблицы приложения 4, это значение равно 2,861, а для доверительной вероятности 0,999 (уровень значимости 0,001) – 3,883. Поскольку 6,47 > 3,883, мы можем сделать вывод о том, что изучаемое лекарство эффективно не только на уровне 0,05, т.е. допуская что вероятность ошибки не больше 5%, но и на уровне 0,001, т.е. вероятность того, что наш вывод не верен не превышает 0,1% !!!
. Следовательно, наблюдаемые различия в артериальном давлении действительно существуют. В настоящий момент мы делаем этот вывод на уровне значимости 0,05. Но теперь, когда мы имеем экспериментальное значение распределения Стьюдента, мы можем его сравнить с табличными значениями для других доверительных вероятностей. Посмотрим, например, чему равно табличное значение распределения Стьюдента для доверительной вероятности 0,99 (уровень значимости 0,01). Как следует из таблицы приложения 4, это значение равно 2,861, а для доверительной вероятности 0,999 (уровень значимости 0,001) – 3,883. Поскольку 6,47 > 3,883, мы можем сделать вывод о том, что изучаемое лекарство эффективно не только на уровне 0,05, т.е. допуская что вероятность ошибки не больше 5%, но и на уровне 0,001, т.е. вероятность того, что наш вывод не верен не превышает 0,1% !!!
Приведенные выше расчеты справедливы для связанных выборок. Теперь будем решать ту же задачу (действительно ли есть эффект или полученные различия есть не более чем игра случая) для не связанных выборок.
Рассмотрим, как проверяется гипотеза о неравенстве средних для несвязанных выборок. В этом случае экспериментальное значение распределения Стьюдента можно рассчитать по формуле:
 (14)
(14)
В формуле (14) и соответственно среднее арифметическое для первой выборки и среднее арифметическое для второй выборки. Аналогично - объем первой выборки, - объем второй выборки, s – объединенная оценка среднеквадратичного отклонения двух групп, которая вычисляется по формуле:  (15)
(15)
В формуле (15) - оценка среднеквадратичного отклонения для первой группы, а - для второй. - значение распределения Стьюдента, рассчитанное по экспериментальным данным.
В таблице 3 приведены значения усредненной по всем оценкам успеваемости двух групп студентов в первом семестре. Необходимо определить, можно ли считать, что одна группа училась лучше другой.
Очевидно, что в данном случае мы имеем дело с несвязанными выборками.
Таблица 3
Осредненная успеваемость студентов двух групп за первый семестр.
| № по порядку | Успеваемость в первой группе (средний балл за семестр) | Успеваемость во второй группе (средний балл за семестр) |
| 4,1 | 3,1 | |
| 3,8 | 3,7 | |
| 4,1 | 3,8 | |
| 3,5 | 3,2 | |
| 3,2 | 4,0 | |
| 2,9 | 3,4 | |
| 3,7 | 3,6 | |
| 4,2 | 4,1 | |
| 5,0 | 3,3 | |
| 2,8 | 4,2 | |
| 3,6 | 2,7 | |
| 4,9 | 3,2 | |
| 2,7 | ||
| 3,9 | ||
| N | ||
| 3,82 | 3,49 | |
| s по группам | 0,69 | 0,49 |
| s объединенное среднеквадратичное отклонение | 0,59 |
Рассчитывали по формуле (3), и рассчитывали по формуле (4). Используя формулу (15) рассчитаем s:

Теперь используя формулу (14) рассчитаем экспериментальное значение распределения Стьюдента:

Далее находим теоретическое значение распределения Стьюдента для доверительной вероятности 0,95 и числом степеней свободы . То есть, ищем число, стоящее на пересечении первого столбца таблицы Приложения 4 и 24 строки. Из таблицы следует, что это число равно  .
.
Следовательно, в нашем случае:  , и мы не имеем права говорить, что одна группа учиться лучше (или хуже) другой. Мы вынуждены признать, что различия, наблюдаемые в успеваемости групп, носят случайный характер, а в целом успеваемость в группах одинакова.
, и мы не имеем права говорить, что одна группа учиться лучше (или хуже) другой. Мы вынуждены признать, что различия, наблюдаемые в успеваемости групп, носят случайный характер, а в целом успеваемость в группах одинакова.
Этим заканчивается решение задачи 2. Осталось сделать только два замечания.
Замечание 1 состоит в том, что приведенные выше схемы расчетов справедливы в том случае, если обе выборки сделаны из генеральных совокупностей, распределенных по закону Гаусса.
Замечание 2. Мы отдаем себе отчет в том, что в настоящее время никто в реальных расчетах считать вручную не будет. Однако для закрепления материала очень полезно провести расчеты с использованием калькулятора. Для этих целей ниже приводится полное решение модельной задачи.
Задача Содержание свободного гепарина крови в двух различных возрастных группах принимало следующие значения:
| X 1 (мг%) | 5,7 | 5,9 | 6,3 | 5,6 | 4,1 | 4,0 | 4,5 | 5,0 | 5,1 | 6,7 |
| X 2 (мг%) | 5,1 | 3,2 | 6,0 | 5,1 | 4,9 | 3,8 | 6,2 | 4,5 | 5,6 | 5,8 |
1. Вычислить выборочную среднюю арифметическую, среднеквадратичное отклонение, стандартную ошибку среднего, медиану, коэффициент вариации для каждого ряда и доверительные интервалы для средних. Сравнить средние значения гепарина для двух возрастных групп.
Решение:
Число измерений в каждом ряду n=10.
Выборочная средняя определяется по формуле:

Следовательно для первого ряда она равна:
Найдем дисперсию по формуле: 
Следовательно, для первого ряда выборочная дисперсия равна:
Вычислим среднеквадратичное отклонение  .
.
Вычислим стандартную ошибку среднего 
Для определения медианы (Ме 1 ) по заданным значениям х 1 i строим вариационный ряд:
4,0 4,1 4,5 5,0 5,1 5,6 5,7 5,9 6,3 6,7
При четном числе вариант медиана определится как среднее арифметическое из двух центральных вариант:
 (мг,%)
(мг,%)
Вычислим коэффициент вариации  .
. 
Рссчитаем 95% доверительный интервал для среднего. В нашем случае число измерений 10, а доверительная вероятность 0,95. Входим в таблицу приложения 4. На пересечении столбца 0,95 и девятой строки стоит число t= 2,262.
Следовательно, в нашем случае, , и значит доверительный интервал будет или окончательно  .
.
Проведя аналогичные расчеты для второго ряда получим:

Сравнивая доверительный интервал для среднего первого ряда, с доверительным интервалом для второго ряда, легко увидеть, что они сильно перекрываются. Следовательно, наблюдаемые различия между средними являются случайными и мы должны прийти к заключению, что различий между ними нет.
2. Сравнить средние, используя вычисление экспериментального значения распределения Стьюдента.
В данном случае мы имеем дело с не связанными выборками, поэтому для вычисление экспериментального значения будем использовать следующую формулу:  .
.
Вычислим объединенная оценка среднеквадратичного отклонения двух групп:
Тогда  . Число степеней свободы в нашем случае равно n=10+10-2=18. Итак, входим в таблицы Приложения 4 по восемнадцатой строке и первому столбцу. На пересечении стоит число 2,103. Это число намного больше, чем полученное 0,71. Следовательно, мы приходим к тому же заключению, что средние двух выборок не различаются.
. Число степеней свободы в нашем случае равно n=10+10-2=18. Итак, входим в таблицы Приложения 4 по восемнадцатой строке и первому столбцу. На пересечении стоит число 2,103. Это число намного больше, чем полученное 0,71. Следовательно, мы приходим к тому же заключению, что средние двух выборок не различаются.
Итак, ответ в данном случае, будет выглядеть так: .
На практике большинство случайных величин, на которых воздействует большое количество случайных факторов, подчиняются нормальному закону распределения вероятностей. Поэтому в различных приложениях теории вероятностей этот закон имеет особое значение.
Случайная величина $X$ подчиняется нормальному закону распределения вероятностей, если ее плотность распределения вероятностей имеет следующий вид
$$f\left(x\right)={{1}\over {\sigma \sqrt{2\pi }}}e^{-{{{\left(x-a\right)}^2}\over {2{\sigma }^2}}}$$
Схематически график функции $f\left(x\right)$ представлен на рисунке и имеет название «Гауссова кривая». Справа от этого графика изображена банкнота в 10 марок ФРГ, которая использовалась еще до появления евро. Если хорошо приглядеться, то на этой банкноте можно заметить гауссову кривую и ее первооткрывателя величайшего математика Карла Фридриха Гаусса.
Вернемся к нашей функции плотности $f\left(x\right)$ и дадим кое-какие пояснения относительно параметров распределения $a,\ {\sigma }^2$. Параметр $a$ характеризует центр рассеивания значений случайной величины, то есть имеет смысл математического ожидания. При изменении параметра $a$ и неизмененном параметре ${\sigma }^2$ мы можем наблюдать смещение графика функции $f\left(x\right)$ вдоль оси абсцисс, при этом сам график плотности не меняет своей формы.

Параметр ${\sigma }^2$ является дисперсией и характеризует форму кривой графика плотности $f\left(x\right)$. При изменении параметра ${\sigma }^2$ при неизмененном параметре $a$ мы можем наблюдать, как график плотности меняет свою форму, сжимаясь или растягиваясь, при этом не сдвигаясь вдоль оси абсцисс.

Вероятность попадания нормально распределенной случайной величины в заданный интервал
Как известно, вероятность попадания случайной величины $X$ в интервал $\left(\alpha ;\ \beta \right)$ можно вычислять $P\left(\alpha < X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Для нормального распределения случайной величины $X$ с параметрами $a,\ \sigma $ справедлива следующая формула:
$$P\left(\alpha < X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right)$$
Здесь функция $\Phi \left(x\right)={{1}\over {\sqrt{2\pi }}}\int^x_0{e^{-t^2/2}dt}$ - функция Лапласа. Значения этой функции берутся из . Можно отметить следующие свойства функции $\Phi \left(x\right)$.

1 . $\Phi \left(-x\right)=-\Phi \left(x\right)$, то есть функция $\Phi \left(x\right)$ является нечетной.
2 . $\Phi \left(x\right)$ - монотонно возрастающая функция.
3 . ${\mathop{lim}_{x\to +\infty } \Phi \left(x\right)\ }=0,5$, ${\mathop{lim}_{x\to -\infty } \Phi \left(x\right)\ }=-0,5$.
Для вычисления значений функции $\Phi \left(x\right)$ можно также воспользоваться мастером функция $f_x$ пакета Excel: $\Phi \left(x\right)=НОРМРАСП\left(x;0;1;1\right)-0,5$. Например, вычислим значений функции $\Phi \left(x\right)$ при $x=2$.

Вероятность попадания нормально распределенной случайной величины $X\in N\left(a;\ {\sigma }^2\right)$ в интервал, симметричный относительно математического ожидания $a$, может быть вычислена по формуле
$$P\left(\left|X-a\right| < \delta \right)=2\Phi \left({{\delta }\over {\sigma }}\right).$$
Правило трех сигм . Практически достоверно, что нормально распределенная случайная величина $X$ попадет в интервал $\left(a-3\sigma ;a+3\sigma \right)$.
Пример 1 . Случайная величина $X$ подчинена нормальному закону распределения вероятностей с параметрами $a=2,\ \sigma =3$. Найти вероятность попадания $X$ в интервал $\left(0,5;1\right)$ и вероятность выполнения неравенства $\left|X-a\right| < 0,2$.
Используя формулу
$$P\left(\alpha < X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right),$$
находим $P\left(0,5;1\right)=\Phi \left({{1-2}\over {3}}\right)-\Phi \left({{0,5-2}\over {3}}\right)=\Phi \left(-0,33\right)-\Phi \left(-0,5\right)=\Phi \left(0,5\right)-\Phi \left(0,33\right)=0,191-0,129=0,062$.
$$P\left(\left|X-a\right| < 0,2\right)=2\Phi \left({{\delta }\over {\sigma }}\right)=2\Phi \left({{0,2}\over {3}}\right)=2\Phi \left(0,07\right)=2\cdot 0,028=0,056.$$
Пример 2 . Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 50 условным денежным единицам, и стандартным отклонением, равным 10. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена за акцию будет:
а) более 70 условных денежных единиц?
б) ниже 50 за акцию?
в) между 45 и 58 условными денежными единицами за акцию?
Пусть случайная величина $X$ - цена на акции некоторой компании. По условию $X$ подчинена нормальному закону распределению с параметрами $a=50$ - математическое ожидание, $\sigma =10$ - стандартное отклонение. Вероятность $P\left(\alpha < X < \beta \right)$ попадания $X$ в интервал $\left(\alpha ,\ \beta \right)$ будем находить по формуле:
$$P\left(\alpha < X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right).$$
$$а)\ P\left(X>70\right)=\Phi \left({{\infty -50}\over {10}}\right)-\Phi \left({{70-50}\over {10}}\right)=0,5-\Phi \left(2\right)=0,5-0,4772=0,0228.$$
$$б)\ P\left(X < 50\right)=\Phi \left({{50-50}\over {10}}\right)-\Phi \left({{-\infty -50}\over {10}}\right)=\Phi \left(0\right)+0,5=0+0,5=0,5.$$
$$в)\ P\left(45 < X < 58\right)=\Phi \left({{58-50}\over {10}}\right)-\Phi \left({{45-50}\over {10}}\right)=\Phi \left(0,8\right)-\Phi \left(-0,5\right)=\Phi \left(0,8\right)+\Phi \left(0,5\right)=$$
Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:
- Биномиальный закон распределения
- Пуассоновский закон распределения
- Геометрический закон распределения
- Гипергеометрический закон распределения
Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.
1. Биномиальный закон распределения.
Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$. Фактически, случайная величина $X$ - это число появлений события $A$ в $n$ независимых испытаний . Закон распределения вероятностей случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.
Пример . В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ - числа мальчиков в семье.
Пусть случайная величина $\xi $ - число мальчиков в семье. Значения, которые может принимать $\xi:\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$, где $n=2$ - число независимых испытаний, $p=0,5$ - вероятность появления события в серии из $n$ испытаний. Получаем:
$P\left(\xi =0\right)=C^0_2\cdot {0,5}^0\cdot {\left(1-0,5\right)}^{2-0}={0,5}^2=0,25;$
$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot {\left(1-0,5\right)}^{2-1}=2\cdot 0,5\cdot 0,5=0,5;$
$P\left(\xi =2\right)=C^2_2\cdot {0,5}^2\cdot {\left(1-0,5\right)}^{2-2}={0,5}^2=0,25.$
Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:
$\begin{array}{|c|c|}
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end{array}$
Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _{i=1}^{n}P(\xi _{{\rm i}})=0,25+0,5+0,25=1 $.
Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt{D\left(\xi \right)}=\sqrt{0,5}\approx 0,707$.
2. Закон распределения Пуассона.
Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.
Замечание . Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.
Пример . Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.
Пример . Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.
Пусть дискретная случайная величина $X$ - число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.
$P\left(X=0\right)={{1^0}\over {0!}}\cdot e^{-1}=0,368;$
$P\left(X=1\right)={{1^1}\over {1!}}\cdot e^{-1}=0,368;$
$P\left(X=2\right)={{1^2}\over {2!}}\cdot e^{-1}=0,184;$
$P\left(X=3\right)={{1^3}\over {3!}}\cdot e^{-1}=0,061;$
$P\left(X=4\right)={{1^4}\over {4!}}\cdot e^{-1}=0,015;$
$P\left(X=5\right)={{1^5}\over {5!}}\cdot e^{-1}=0,003;$
$P\left(X=6\right)={{1^6}\over {6!}}\cdot e^{-1}=0,001;$
$P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$
Закон распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & {{{\lambda }^k}\over {k!}}\cdot e^{-\lambda } \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.
3. Геометрический закон распределения.
Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p{\left(1-p\right)}^{k-1},\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.
Пример . Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.
Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.
Пример . На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.
Пусть случайная величина $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^{k-1}$, где: $p=2/5$ - вероятность задержания рыбы через шлюз, $q=1-p=3/5$ - вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.
$P\left(X=1\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^0={{2}\over {5}}=0,4;$
$P\left(X=2\right)={{2}\over {5}}\cdot {{3}\over {5}}={{6}\over {25}}=0,24;$
$P\left(X=3\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^2={{2}\over {5}}\cdot {{9}\over {25}}={{18}\over {125}}=0,144;$
$P\left(X=4\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^3+{\left({{3}\over {5}}\right)}^4={{27}\over {125}}=0,216.$
$\begin{array}{|c|c|}
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end{array}$
Математическое ожидание:
$M\left(X\right)=\sum^n_{i=1}{x_ip_i}=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$
Дисперсия:
$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2=}0,4\cdot {\left(1-2,176\right)}^2+0,24\cdot {\left(2-2,176\right)}^2+0,144\cdot {\left(3-2,176\right)}^2+$
$+\ 0,216\cdot {\left(4-2,176\right)}^2\approx 1,377.$
Среднее квадратическое отклонение:
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{1,377}\approx 1,173.$
4. Гипергеометрический закон распределения.
Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ - число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:
$P\left(X=k\right)={{C^k_mC^{n-k}_{N-m}}\over {C^n_N}}$
Замечание . Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.
$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК . Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.
Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}$.
Пример . В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.
а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;
б) Найдите числовые характеристики этого распределения.
Пусть случайная величина $X$ - число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ - размер совокупности, $m=5$ - число успехов в совокупности, $n=3$ - размер выборки, $k=0,\ 1,\ 2,\ 3$ - число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)={C_{m}^{k} \cdot C_{N-m}^{n-k} \over C_{N}^{n} } $. Имеем:
$P\left(X=0\right)={{C^0_5\cdot C^3_3}\over {C^3_8}}={{1}\over {56}}\approx 0,018;$
$P\left(X=1\right)={{C^1_5\cdot C^2_3}\over {C^3_8}}={{15}\over {56}}\approx 0,268;$
$P\left(X=2\right)={{C^2_5\cdot C^1_3}\over {C^3_8}}={{15}\over {28}}\approx 0,536;$
$P\left(X=3\right)={{C^3_5\cdot C^0_3}\over {C^3_8}}={{5}\over {28}}\approx 0,179.$
Тогда ряд распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end{array}$
Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.
$M\left(X\right)={{nm}\over {N}}={{3\cdot 5}\over {8}}={{15}\over {8}}=1,875.$
$D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}={{3\cdot 5\cdot \left(1-{{5}\over {8}}\right)\cdot \left(1-{{3}\over {8}}\right)}\over {8-1}}={{225}\over {448}}\approx 0,502.$
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{0,502}\approx 0,7085.$
1.2.4. Случайные величины и их распределения
Распределения случайных величин и функции распределения . Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией Р(Х = х), ставящей каждому возможному значению х случайной величины Х вероятность того, что Х = х .
Второе
– если случайная величина принимает бесконечно много значений. Это возможно
лишь тогда, когда вероятностное пространство, на котором определена случайная величина,
состоит из бесконечного числа элементарных событий. Тогда распределение
задается набором вероятностей P(a <
X
P(a <
X
Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и, наоборот, функция распределения – по распределению.
Используемые в вероятностно-статистических методах принятия решений и других прикладных исследованиях функции распределения бывают либо дискретными, либо непрерывными, либо их комбинациями.
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными). Их график имеет вид ступенчатой лестницы (рис. 1).
Пример 1. Число Х дефектных изделий в партии принимает значение 0 с вероятностью 0,3, значение 1 с вероятностью 0,4, значение 2 с вероятностью 0,2 и значение 3 с вероятностью 0,1. График функции распределения случайной величины Х изображен на рис.1.
Рис.1. График функции распределения числа дефектных изделий.
Непрерывные функции распределения не имеют скачков. Они монотонно возрастают при увеличении аргумента – от 0 при до 1 при . Случайные величины, имеющие непрерывные функции распределения, называют непрерывными.
Непрерывные функции распределения, используемые в вероятностно-статистических методах принятия решений, имеют производные. Первая производная f(x) функции распределения F(x) называется плотностью вероятности,
По плотности вероятности можно определить функцию распределения:
![]()
Для любой функции распределения
Перечисленные свойства функций распределения постоянно используются в вероятностно-статистических методах принятия решений. В частности, из последнего равенства вытекает конкретный вид констант в формулах для плотностей вероятностей, рассматриваемых ниже.
Пример 2. Часто используется следующая функция распределения:
 (1)
(1)
где a и b – некоторые числа, a. Найдем плотность вероятности этой функции распределения:

(в точках x = a и x = b производная функции F(x) не существует).
Случайная величина с функцией распределения (1) называется «равномерно распределенной на отрезке [a; b ]».
Смешанные функции распределения встречаются, в частности, тогда, когда наблюдения в какой-то момент прекращаются. Например, при анализе статистических данных, полученных при использовании планов испытаний на надежность, предусматривающих прекращение испытаний по истечении некоторого срока. Или при анализе данных о технических изделиях, потребовавших гарантийного ремонта.
Пример 3. Пусть, например, срок службы электрической лампочки – случайная величина с функцией распределения F(t), а испытание проводится до выхода лампочки из строя, если это произойдет менее чем за 100 часов от начала испытаний, или до момента t 0 = 100 часов. Пусть G(t) – функция распределения времени эксплуатации лампочки в исправном состоянии при этом испытании. Тогда

Функция G(t) имеет скачок в точке t 0 , поскольку соответствующая случайная величина принимает значение t 0 с вероятностью 1-F(t 0)> 0.
Характеристики случайных величин. В вероятностно-статистических методах принятия решений используется ряд характеристик случайных величин, выражающихся через функции распределения и плотности вероятностей.
При описании дифференциации доходов, при нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как «квантиль порядка р », где 0 < p < 1 (обозначается х р ). Квантиль порядка р – значение случайной величины, для которого функция распределения принимает значение р или имеет место «скачок» со значения меньше р до значения больше р (рис.2). Может случиться, что это условие выполняется для всех значений х, принадлежащих этому интервалу (т.е. функция распределения постоянна на этом интервале и равна р ). Тогда каждое такое значение называется «квантилем порядка р ». Для непрерывных функций распределения, как правило, существует единственный квантиль х р порядка р (рис.2), причем
F(x p) = p . (2)

Рис.2. Определение квантиля х р порядка р .
Пример 4. Найдем квантиль х р порядка р для функции распределения F(x) из (1).
При 0 < p < 1 квантиль х р находится из уравнения
т.е. х р = a + p(b – a) = a(1- p) +bp . При p = 0 любое x < a является квантилем порядка p = 0. Квантилем порядка p = 1 является любое число x > b .
Для дискретных распределений, как правило, не существует х р , удовлетворяющих уравнению (2). Точнее, если распределение случайной величины дается табл.1, где x 1 < x 2 < … < x k , то равенство (2), рассматриваемое как уравнение относительно х р , имеет решения только для k значений p , а именно,
p = p 1 ,
p = p 1 + p 2 ,
p = p 1 + p 2 + p 3 ,
p = p 1 + p 2 + … + p m , 3 < m < k ,
p = p 1 + p 2 + … + p k .
Таблица 1.
Распределение дискретной случайной величины
Для перечисленных k значений вероятности p решение х р уравнения (2) неединственно, а именно,
F(x) = p 1 + p 2 + … + p m
для всех х таких, что x m < x < x m+1 . Т.е. х р – любое число из интервала (x m ; x m+1 ]. Для всех остальных р из промежутка (0;1), не входящих в перечень (3), имеет место «скачок» со значения меньше р до значения больше р . А именно, если
p 1 + p 2 + … + p m
то х р = x m+1 .
Рассмотренное свойство дискретных распределений создает значительные трудности при табулировании и использовании подобных распределений, поскольку невозможным оказывается точно выдержать типовые численные значения характеристик распределения. В частности, это так для критических значений и уровней значимости непараметрических статистических критериев (см. ниже), поскольку распределения статистик этих критериев дискретны.
Большое значение в статистике имеет квантиль порядка р = ½. Он называется медианой (случайной величины Х или ее функции распределения F(x)) и обозначается Me(X). В геометрии есть понятие «медиана» - прямая, проходящая через вершину треугольника и делящая противоположную его сторону пополам. В математической статистике медиана делит пополам не сторону треугольника, а распределение случайной величины: равенство F(x 0,5) = 0,5 означает, что вероятность попасть левее x 0,5 и вероятность попасть правее x 0,5 (или непосредственно в x 0,5 ) равны между собой и равны ½, т.е.
P (X < x 0,5) = P (X > x 0,5) = ½.
Медиана указывает «центр» распределения. С точки зрения одной из современных концепций – теории устойчивых статистических процедур – медиана является более хорошей характеристикой случайной величины, чем математическое ожидание . При обработке результатов измерений в порядковой шкале (см. главу о теории измерений) медианой можно пользоваться, а математическим ожиданием – нет.
Ясный смысл имеет такая характеристика случайной величины, как мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
Если x 0 – мода случайной величины с плотностью f(x), то, как известно из дифференциального исчисления, .
У случайной величины может быть много мод. Так, для равномерного распределения (1) каждая точка х такая, что a < x < b , является модой. Однако это исключение. Большинство случайных величин, используемых в вероятностно-статистических методах принятия решений и других прикладных исследованиях, имеют одну моду. Случайные величины, плотности, распределения, имеющие одну моду, называются унимодальными.
Математическое ожидание для дискретных случайных величин с конечным числом значений рассмотрено в главе «События и вероятности». Для непрерывной случайной величины Х математическое ожидание М(Х) удовлетворяет равенству
![]()
являющемуся аналогом формулы (5) из утверждения 2 главы «События и вероятности».
Пример 5. Математическое ожидание для равномерно распределенной случайной величины Х равно
Для рассматриваемых в настоящей главе случайных величин верны все те свойства математических ожиданий и дисперсий, которые были рассмотрены ранее для дискретных случайных величин с конечным числом значений. Однако доказательства этих свойств не приводим, поскольку они требуют углубления в математические тонкости, не являющегося необходимым для понимания и квалифицированного применения вероятностно-статистических методов принятия решений.
Замечание. В настоящем учебнике сознательно обходятся математические тонкости, связанные, в частности, с понятиями измеримых множеств и измеримых функций, -алгебры событий и т.п. Желающим освоить эти понятия необходимо обратиться к специальной литературе, в частности, к энциклопедии .
Каждая из трех характеристик – математическое ожидание, медиана, мода – описывает «центр» распределения вероятностей. Понятие «центр» можно определять разными способами – отсюда три разные характеристики. Однако для важного класса распределений – симметричных унимодальных – все три характеристики совпадают.
Плотность распределения f(x) – плотность симметричного распределения, если найдется число х 0 такое, что
![]() . (3)
. (3)
Равенство (3) означает, что график функции y = f(x) симметричен относительно вертикальной прямой, проходящей через центр симметрии х = х 0 . Из (3) следует, что функция симметричного распределения удовлетворяет соотношению
![]() (4)
(4)
Для симметричного распределения с одной модой математическое ожидание, медиана и мода совпадают и равны х 0 .
Наиболее важен случай симметрии относительно 0, т.е. х 0 = 0. Тогда (3) и (4) переходят в равенства
![]() (6)
(6)
соответственно. Приведенные соотношения показывают, что симметричные распределения нет необходимости табулировать при всех х , достаточно иметь таблицы при x > x 0 .
Отметим еще одно свойство симметричных распределений, постоянно используемое в вероятностно-статистических методах принятия решений и других прикладных исследованиях. Для непрерывной функции распределения
P(|X|< a) = P(-a < X < a) = F(a) – F(-a),
где F – функция распределения случайной величины Х . Если функция распределения F симметрична относительно 0, т.е. для нее справедлива формула (6), то
P(|X|< a) = 2F(a) – 1.
Часто используют другую формулировку рассматриваемого утверждения: если
![]() .
.
Если и - квантили порядка и соответственно (см. (2)) функции распределения, симметричной относительно 0, то из (6) следует, что
От характеристик положения – математического ожидания, медианы, моды – перейдем к характеристикам разброса случайной величины Х : дисперсии , среднему квадратическому отклонению и коэффициенту вариации v . Определение и свойства дисперсии для дискретных случайных величин рассмотрены в предыдущей главе. Для непрерывных случайных величин
Среднее квадратическое отклонение – это неотрицательное значение квадратного корня из дисперсии:
Коэффициент вариации – это отношение среднего квадратического отклонения к математическому ожиданию:
Коэффициент вариации применяется при M(X)> 0. Он измеряет разброс в относительных единицах, в то время как среднее квадратическое отклонение – в абсолютных.
Пример 6. Для равномерно распределенной случайной величины Х найдем дисперсию, среднеквадратическое отклонение и коэффициент вариации. Дисперсия равна:

Замена переменной дает возможность записать:
где c = (b – a )/ 2. Следовательно, среднее квадратическое отклонение равно а коэффициент вариации таков:
По каждой случайной величине Х определяют еще три величины – центрированную Y , нормированную V и приведенную U . Центрированная случайная величина Y – это разность между данной случайной величиной Х и ее математическим ожиданием М(Х), т.е. Y = Х – М(Х). Математическое ожидание центрированной случайной величины Y равно 0, а дисперсия – дисперсии данной случайной величины: М(Y ) = 0, D (Y ) = D (X ). Функция распределения F Y (x ) центрированной случайной величины Y связана с функцией распределения F (x ) исходной случайной величины X соотношением:
F Y (x ) = F (x + M (X )).
Для плотностей этих случайных величин справедливо равенство
f Y (x ) = f (x + M (X )).
Нормированная случайная величина V – это отношение данной случайной величины Х к ее среднему квадратическому отклонению , т.е. . Математическое ожидание и дисперсия нормированной случайной величины V выражаются через характеристики Х так:
![]() ,
,
где v – коэффициент вариации исходной случайной величины Х . Для функции распределения F V (x ) и плотности f V (x ) нормированной случайной величины V имеем:
где F (x ) – функция распределения исходной случайной величины Х , а f (x ) – ее плотность вероятности.
Приведенная случайная величина U – это центрированная и нормированная случайная величина:
![]() .
.
Для приведенной случайной величины
Нормированные, центрированные и
приведенные случайные величины постоянно используются как в теоретических
исследованиях, так и в алгоритмах, программных продуктах,
нормативно-технической и инструктивно-методической документации. В частности,
потому, что равенства ![]() позволяют упростить
обоснования методов, формулировки теорем и расчетные формулы.
позволяют упростить
обоснования методов, формулировки теорем и расчетные формулы.
Используются преобразования случайных величин и более общего плана. Так, если Y = aX + b , где a и b – некоторые числа, то
Пример 7. Если то Y – приведенная случайная величина, и формулы (8) переходят в формулы (7).
С каждой случайной величиной Х можно связать множество случайных величин Y , заданных формулой Y = aX + b при различных a > 0 и b . Это множество называют масштабно-сдвиговым семейством , порожденным случайной величиной Х . Функции распределения F Y (x ) составляют масштабно сдвиговое семейство распределений, порожденное функцией распределения F (x ). Вместо Y = aX + b часто используют запись
![]()
Число с называют параметром сдвига, а число d - параметром масштаба. Формула (9) показывает, что Х – результат измерения некоторой величины – переходит в У – результат измерения той же величины, если начало измерения перенести в точку с , а затем использовать новую единицу измерения, в d раз большую старой.
Для масштабно-сдвигового семейства (9) распределение Х называют стандартным. В вероятностно-статистических методах принятия решений и других прикладных исследованиях используют стандартное нормальное распределение, стандартное распределение Вейбулла-Гнеденко, стандартное гамма-распределение и др. (см. ниже).
Применяют и другие преобразования случайных величин. Например, для положительной случайной величины Х рассматривают Y = lg X , где lg X – десятичный логарифм числа Х . Цепочка равенств
F Y (x) = P(lg X < x) = P(X < 10 x) = F(10 x)
связывает функции распределения Х и Y .
При обработке данных используют такие характеристики случайной величины Х как моменты порядка q , т.е. математические ожидания случайной величины X q , q = 1, 2, … Так, само математическое ожидание – это момент порядка 1. Для дискретной случайной величины момент порядка q может быть рассчитан как
![]()
Для непрерывной случайной величины
![]()
Моменты порядка q называют также начальными моментами порядка q , в отличие от родственных характеристик – центральных моментов порядка q , задаваемых формулой
Так, дисперсия – это центральный момент порядка 2.
Нормальное распределение и центральная предельная теорема. В вероятностно-статистических методах принятия решений часто идет речь о нормальном распределении. Иногда его пытаются использовать для моделирования распределения исходных данных (эти попытки не всегда являются обоснованными – см. ниже). Более существенно, что многие методы обработки данных основаны на том, что расчетные величины имеют распределения, близкие к нормальному.
Пусть X 1 , X 2 ,…, X n M (X i ) = m и дисперсиями D (X i ) = , i = 1, 2,…, n ,… Как следует из результатов предыдущей главы,
Рассмотрим приведенную случайную
величину U n
для суммы ![]() , а именно,
, а именно,
![]()
Как следует из формул (7), M (U n ) = 0, D (U n ) = 1.
(для одинаково распределенных слагаемых). Пусть X 1 , X 2 ,…, X n , …– независимые одинаково распределенные случайные величины с математическими ожиданиями M (X i ) = m и дисперсиями D (X i ) = , i = 1, 2,…, n ,… Тогда для любого х существует предел
![]()
где Ф(х) – функция стандартного нормального распределения.
Подробнее о функции Ф(х) – ниже (читается «фи от икс», поскольку Ф – греческая прописная буква «фи»).
Центральная предельная теорема (ЦПТ) носит свое название по той причине, что она является центральным, наиболее часто применяющимся математическим результатом теории вероятностей и математической статистики. История ЦПТ занимает около 200 лет – с 1730 г., когда английский математик А.Муавр (1667-1754) опубликовал первый результат, относящийся к ЦПТ (см. ниже о теореме Муавра-Лапласа), до двадцатых – тридцатых годов ХХ в., когда финн Дж.У. Линдеберг, француз Поль Леви (1886-1971), югослав В. Феллер (1906-1970), русский А.Я. Хинчин (1894-1959) и другие ученые получили необходимые и достаточные условия справедливости классической центральной предельной теоремы.
Развитие рассматриваемой тематики на этом отнюдь не прекратилось – изучали случайные величины, не имеющие дисперсии, т.е. те, для которых
![]()
(академик Б.В.Гнеденко и др.), ситуацию, когда суммируются случайные величины (точнее, случайные элементы) более сложной природы, чем числа (академики Ю.В.Прохоров, А.А.Боровков и их соратники), и т.д.
Функция распределения Ф(х) задается равенством
![]() ,
,
где - плотность стандартного нормального распределения, имеющая довольно сложное выражение:
![]() .
.
Здесь =3,1415925… - известное в геометрии число, равное отношению длины окружности к диаметру, e = 2,718281828… - основание натуральных логарифмов (для запоминания этого числа обратите внимание, что 1828 – год рождения писателя Л.Н.Толстого). Как известно из математического анализа,
![]()
При обработке результатов наблюдений функцию нормального распределения не вычисляют по приведенным формулам, а находят с помощью специальных таблиц или компьютерных программ. Лучшие на русском языке «Таблицы математической статистики» составлены членами-корреспондентами АН СССР Л.Н. Большевым и Н.В.Смирновым .
Вид плотности стандартного нормального распределения вытекает из математической теории, которую не имеем возможности здесь рассматривать, равно как и доказательство ЦПТ.
Для иллюстрации приводим небольшие таблицы функции распределения Ф(х) (табл.2) и ее квантилей (табл.3). Функция Ф(х) симметрична относительно 0, что отражается в табл.2-3.
Таблица 2.
Функция стандартного нормального распределения.
Если случайная величина Х имеет функцию распределения Ф(х), то М(Х) = 0, D (X ) = 1. Это утверждение доказывается в теории вероятностей, исходя из вида плотности вероятностей . Оно согласуется с аналогичным утверждением для характеристик приведенной случайной величины U n , что вполне естественно, поскольку ЦПТ утверждает, что при безграничном возрастании числа слагаемых функция распределения U n стремится к функции стандартного нормального распределения Ф(х), причем при любом х .
Таблица 3.
Квантили стандартного нормального распределения.
Квантиль порядка р |
Квантиль порядка р |
||
Введем понятие семейства нормальных распределений. По определению нормальным распределением называется распределение случайной величины Х , для которой распределение приведенной случайной величины есть Ф(х). Как следует из общих свойств масштабно-сдвиговых семейств распределений (см. выше), нормальное распределение – это распределение случайной величины
где Х – случайная величина с распределением Ф(Х), причем m = M (Y ), = D (Y ). Нормальное распределение с параметрами сдвига m и масштаба обычно обозначается N (m , ) (иногда используется обозначение N (m , ) ).
Как следует из (8), плотность вероятности нормального распределения N (m , ) есть

Нормальные распределения образуют масштабно-сдвиговое семейство. При этом параметром масштаба является d = 1/ , а параметром сдвига c = - m / .
Для центральных моментов третьего и четвертого порядка нормального распределения справедливы равенства
![]()
Эти равенства лежат в основе классических методов проверки того, что результаты наблюдений подчиняются нормальному распределению. В настоящее время нормальность обычно рекомендуется проверять по критерию W Шапиро – Уилка. Проблема проверки нормальности обсуждается ниже.
Если
случайные величины Х 1
и Х 2
имеют функции
распределения N
(m
1
, 1)
и N
(m
2
, 2)
соответственно, то Х 1
+ Х 2
имеет распределение ![]() Следовательно, если
случайные величины X
1
,
X
2
,…,
X n
N
(m
, )
, то их среднее арифметическое
Следовательно, если
случайные величины X
1
,
X
2
,…,
X n
N
(m
, )
, то их среднее арифметическое
![]()
имеет распределение N (m , ) . Эти свойства нормального распределения постоянно используются в различных вероятностно-статистических методах принятия решений, в частности, при статистическом регулировании технологических процессов и в статистическом приемочном контроле по количественному признаку.
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных.
Распределение (хи - квадрат) – распределение случайной величины
где случайные величины X 1 , X 2 ,…, X n независимы и имеют одно и тоже распределение N (0,1). При этом число слагаемых, т.е. n , называется «числом степеней свободы» распределения хи – квадрат.
Распределение t Стьюдента – это распределение случайной величины
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N (0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента. Это распределение было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов принятия решений.
Распределение Фишера – это распределение случайной величины
где случайные величины Х 1 и Х 2 независимы и имеют распределения хи – квадрат с числом степеней свободы k 1 и k 2 соответственно. При этом пара (k 1 , k 2 ) – пара «чисел степеней свободы» распределения Фишера, а именно, k 1 – число степеней свободы числителя, а k 2 – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
Выражения для функций распределения хи - квадрат, Стьюдента и Фишера, их плотностей и характеристик, а также таблицы можно найти в специальной литературе (см., например, ).
Как уже отмечалось, нормальные распределения в настоящее время часто используют в вероятностных моделях в различных прикладных областях. В чем причина такой широкой распространенности этого двухпараметрического семейства распределений? Она проясняется следующей теоремой.
Центральная предельная теорема (для разнораспределенных слагаемых). Пусть X 1 , X 2 ,…, X n ,… - независимые случайные величины с математическими ожиданиями М(X 1 ), М(X 2 ),…, М(X n), … и дисперсиями D (X 1 ), D (X 2 ),…, D (X n), … соответственно. Пусть
Тогда при справедливости некоторых условий, обеспечивающих малость вклада любого из слагаемых в U n ,
![]()
для любого х .
Условия, о которых идет речь, не будем здесь формулировать. Их можно найти в специальной литературе (см., например, ). «Выяснение условий, при которых действует ЦПТ, составляет заслугу выдающихся русских ученых А.А.Маркова (1857-1922) и, в особенности, А.М.Ляпунова (1857-1918)» .
Центральная предельная теорема показывает, что в случае, когда результат измерения (наблюдения) складывается под действием многих причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно , т.е. путем сложения, то распределение результата измерения (наблюдения) близко к нормальному.
Иногда считают, что для нормальности распределения достаточно того, что результат измерения (наблюдения) Х формируется под действием многих причин, каждая из которых оказывает малое воздействие. Это не так. Важно, как эти причины действуют. Если аддитивно – то Х имеет приближенно нормальное распределение. Если мультипликативно (т.е. действия отдельных причин перемножаются, а не складываются), то распределение Х близко не к нормальному, а к т.н. логарифмически нормальному, т.е. не Х , а lg X имеет приблизительно нормальное распределение. Если же нет оснований считать, что действует один из этих двух механизмов формирования итогового результата (или какой-либо иной вполне определенный механизм), то про распределение Х ничего определенного сказать нельзя.
Из сказанного вытекает, что в конкретной прикладной задаче нормальность результатов измерений (наблюдений), как правило, нельзя установить из общих соображений, ее следует проверять с помощью статистических критериев. Или же использовать непараметрические статистические методы, не опирающиеся на предположения о принадлежности функций распределения результатов измерений (наблюдений) к тому или иному параметрическому семейству.
Непрерывные распределения, используемые в вероятностно-статистических методах принятия решений. Кроме масштабно-сдвигового семейства нормальных распределений, широко используют ряд других семейств распределения – логарифмически нормальных, экспоненциальных, Вейбулла-Гнеденко, гамма-распределений. Рассмотрим эти семейства.
Случайная величина Х имеет логарифмически нормальное распределение, если случайная величина Y = lg X имеет нормальное распределение. Тогда Z = ln X = 2,3026…Y также имеет нормальное распределение N (a 1 ,σ 1) , где ln X - натуральный логарифм Х . Плотность логарифмически нормального распределения такова:

Из центральной предельной теоремы следует, что произведение X = X 1 X 2 … X n независимых положительных случайных величин X i , i = 1, 2,…, n , при больших n можно аппроксимировать логарифмически нормальным распределением. В частности, мультипликативная модель формирования заработной платы или дохода приводит к рекомендации приближать распределения заработной платы и дохода логарифмически нормальными законами. Для России эта рекомендация оказалась обоснованной - статистические данные подтверждают ее.
Имеются и другие вероятностные модели, приводящие к логарифмически нормальному закону. Классический пример такой модели дан А.Н.Колмогоровым , который из физически обоснованной системы постулатов вывел заключение о том, что размеры частиц при дроблении кусков руды, угля и т.п. на шаровых мельницах имеют логарифмически нормальное распределение.
Перейдем к другому семейству распределений, широко используемому в различных вероятностно-статистических методах принятия решений и других прикладных исследованиях, - семейству экспоненциальных распределений. Начнем с вероятностной модели, приводящей к таким распределениям. Для этого рассмотрим "поток событий", т.е. последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток отказов оборудования в технологической цепочке; поток отказов изделий при испытаниях продукции; поток обращений клиентов в отделение банка; поток покупателей, обращающихся за товарами и услугами, и т.д. В теории потоков событий справедлива теорема, аналогичная центральной предельной теореме, но в ней речь идет не о суммировании случайных величин, а о суммировании потоков событий. Рассматривается суммарный поток, составленный из большого числа независимых потоков, ни один из которых не оказывает преобладающего влияния на суммарный поток. Например, поток вызовов, поступающих на телефонную станцию, слагается из большого числа независимых потоков вызовов, исходящих от отдельных абонентов. Доказано , что в случае, когда характеристики потоков не зависят от времени, суммарный поток полностью описывается одним числом - интенсивностью потока. Для суммарного потока рассмотрим случайную величину Х - длину промежутка времени между последовательными событиями. Ее функция распределения имеет вид
 (10)
(10)
Это распределение называется экспоненциальным распределением, т.к. в формуле (10) участвует экспоненциальная функция e -λ x . Величина 1/λ - масштабный параметр. Иногда вводят и параметр сдвига с , экспоненциальным называют распределение случайной величины Х + с , где распределение Х задается формулой (10).
Экспоненциальные распределения - частный случай т. н. распределений Вейбулла - Гнеденко. Они названы по фамилиям инженера В. Вейбулла, введшего эти распределения в практику анализа результатов усталостных испытаний, и математика Б.В.Гнеденко (1912-1995), получившего такие распределения в качестве предельных при изучении максимального из результатов испытаний. Пусть Х - случайная величина, характеризующая длительность функционирования изделия, сложной системы, элемента (т.е. ресурс, наработку до предельного состояния и т.п.), длительность функционирования предприятия или жизни живого существа и т.д. Важную роль играет интенсивность отказа
![]() (11)
(11)
где F (x ) и f (x ) - функция распределения и плотность случайной величины Х .
Опишем типичное поведение интенсивности отказа. Весь интервал времени можно разбить на три периода. На первом из них функция λ(х) имеет высокие значения и явную тенденцию к убыванию (чаще всего она монотонно убывает). Это можно объяснить наличием в рассматриваемой партии единиц продукции с явными и скрытыми дефектами, которые приводят к относительно быстрому выходу из строя этих единиц продукции. Первый период называют "периодом приработки" (или "обкатки"). Именно на него обычно распространяется гарантийный срок.
Затем наступает период нормальной эксплуатации, характеризующийся приблизительно постоянной и сравнительно низкой интенсивностью отказов. Природа отказов в этот период носит внезапный характер (аварии, ошибки эксплуатационных работников и т.п.) и не зависит от длительности эксплуатации единицы продукции.
Наконец, последний период эксплуатации - период старения и износа. Природа отказов в этот период - в необратимых физико-механических и химических изменениях материалов, приводящих к прогрессирующему ухудшению качества единицы продукции и окончательному выходу ее из строя.
Каждому периоду соответствует свой вид функции λ(х) . Рассмотрим класс степенных зависимостей
λ(х) = λ 0 bx b -1 , (12)
где λ 0 > 0 и b > 0 - некоторые числовые параметры. Значения b < 1, b = 0 и b > 1 отвечают виду интенсивности отказов в периоды приработки, нормальной эксплуатации и старения соответственно.
Соотношение (11) при заданной интенсивности отказа λ(х) - дифференциальное уравнение относительно функции F (x ). Из теории дифференциальных уравнений следует, что
 (13)
(13)
Подставив (12) в (13), получим, что
 (14)
(14)
Распределение, задаваемое формулой (14) называется распределением Вейбулла - Гнеденко. Поскольку
то из формулы (14) следует, что величина а , задаваемая формулой (15), является масштабным параметром. Иногда вводят и параметр сдвига, т.е. функциями распределения Вейбулла - Гнеденко называют F (x - c ), где F (x ) задается формулой (14) при некоторых λ 0 и b .
Плотность распределения Вейбулла - Гнеденко имеет вид
 (16)
(16)
где a > 0 - параметр масштаба, b > 0 - параметр формы, с - параметр сдвига. При этом параметр а из формулы (16) связан с параметром λ 0 из формулы (14) соотношением, указанным в формуле (15).
Экспоненциальное распределение - весьма частный случай распределения Вейбулла - Гнеденко, соответствующий значению параметра формы b = 1.
Распределение Вейбулла - Гнеденко применяется также при построении вероятностных моделей ситуаций, в которых поведение объекта определяется "наиболее слабым звеном". Подразумевается аналогия с цепью, сохранность которой определяется тем ее звеном, которое имеет наименьшую прочность. Другими словами, пусть X 1 , X 2 ,…, X n - независимые одинаково распределенные случайные величины,
X(1) = min (X 1 , X 2 ,…, X n ), X(n) = max (X 1 , X 2 ,…, X n ).
В ряде прикладных задач большую роль играют X (1) и X (n ) , в частности, при исследовании максимально возможных значений ("рекордов") тех или иных значений, например, страховых выплат или потерь из-за коммерческих рисков, при изучении пределов упругости и выносливости стали, ряда характеристик надежности и т.п. Показано, что при больших n распределения X (1) и X (n ) , как правило, хорошо описываются распределениями Вейбулла - Гнеденко. Основополагающий вклад в изучение распределений X (1) и X (n ) внес советский математик Б.В.Гнеденко. Использованию полученных результатов в экономике, менеджменте, технике и других областях посвящены труды В. Вейбулла, Э. Гумбеля, В.Б. Невзорова, Э.М. Кудлаева и многих иных специалистов.
Перейдем к семейству гамма-распределений. Они широко применяются в экономике и менеджменте, теории и практике надежности и испытаний, в различных областях техники, метеорологии и т.д. В частности, гамма-распределению подчинены во многих ситуациях такие величины, как общий срок службы изделия, длина цепочки токопроводящих пылинок, время достижения изделием предельного состояния при коррозии, время наработки до k -го отказа, k = 1, 2, …, и т.д. Продолжительность жизни больных хроническими заболеваниями, время достижения определенного эффекта при лечении в ряде случаев имеют гамма-распределение. Это распределение наиболее адекватно для описания спроса в экономико-математических моделях управления запасами (логистики).
Плотность гамма-распределения имеет вид
 (17)
(17)
Плотность вероятности в формуле (17) определяется тремя параметрами a , b , c , где a >0, b >0. При этом a является параметром формы, b - параметром масштаба и с - параметром сдвига. Множитель 1/Γ(а) является нормировочным, он введен, чтобы
![]()
Здесь Γ(а) - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (17),

При фиксированном а формула (17) задает масштабно-сдвиговое семейство распределений, порождаемое распределением с плотностью
 (18)
(18)
Распределение вида (18) называется стандартным гамма-распределением. Оно получается из формулы (17) при b = 1 и с = 0.
Частным случаем гамма-распределений при а = 1 являются экспоненциальные распределения (с λ = 1/ b ). При натуральном а и с =0 гамма-распределения называются распределениями Эрланга. С работ датского ученого К.А.Эрланга (1878-1929), сотрудника Копенгагенской телефонной компании, изучавшего в 1908-1922 гг. функционирование телефонных сетей, началось развитие теории массового обслуживания. Эта теория занимается вероятностно-статистическим моделированием систем, в которых происходит обслуживание потока заявок, с целью принятия оптимальных решений. Распределения Эрланга используют в тех же прикладных областях, в которых применяют экспоненциальные распределения. Это основано на следующем математическом факте: сумма k независимых случайных величин, экспоненциально распределенных с одинаковыми параметрами λ и с , имеет гамма-распределение с параметром формы а = k , параметром масштаба b = 1/λ и параметром сдвига kc . При с = 0 получаем распределение Эрланга.
Если случайная величина X имеет гамма-распределение с параметром формы а таким, что d = 2 a - целое число, b = 1 и с = 0, то 2Х имеет распределение хи-квадрат с d степенями свободы.
Случайная величина X с гвмма-распределением имеет следующие характеристики:
Математическое ожидание М(Х) = ab + c ,
Дисперсию D (X ) = σ 2 = ab 2 ,
Коэффициент вариации
Асимметрию ![]()
Эксцесс ![]()
Нормальное распределение - предельный случай гамма-распределения. Точнее, пусть Z - случайная величина, имеющая стандартное гамма-распределение, заданное формулой (18). Тогда
![]()
для любого действительного числа х , где Ф(х) - функция стандартного нормального распределения N (0,1).
В прикладных исследованиях используются и другие параметрические семейства распределений, из которых наиболее известны система кривых Пирсона, ряды Эджворта и Шарлье. Здесь они не рассматриваются.
Дискретные распределения, используемые в вероятностно-статистических методах принятия решений. Наиболее часто используют три семейства дискретных распределений - биномиальных, гипергеометрических и Пуассона, а также некоторые другие семейства - геометрических, отрицательных биномиальных, мультиномиальных, отрицательных гипергеометрических и т.д.
Как уже говорилось, биномиальное распределение имеет место при независимых испытаниях, в каждом из которых с вероятностью р появляется событие А . Если общее число испытаний n задано, то число испытаний Y , в которых появилось событие А , имеет биномиальное распределение. Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой
![]()
Число сочетаний из n элементов по y , известное из комбинаторики. Для всех y , кроме 0, 1, 2, …, n , имеем P (Y = y )= 0. Биномиальное распределение при фиксированном объеме выборки n задается параметром p , т.е. биномиальные распределения образуют однопараметрическое семейство. Они применяются при анализе данных выборочных исследований , в частности, при изучении предпочтений потребителей, выборочном контроле качества продукции по планам одноступенчатого контроля, при испытаниях совокупностей индивидуумов в демографии, социологии, медицине, биологии и др.
Если Y 1 и Y 2 - независимые биномиальные случайные величины с одним и тем же параметром p 0 , определенные по выборкам с объемами n 1 и n 2 соответственно, то Y 1 + Y 2 - биномиальная случайная величина, имеющая распределение (19) с р = p 0 и n = n 1 + n 2 . Это замечание расширяет область применимости биномиального распределения, позволяя объединять результаты нескольких групп испытаний, когда есть основания полагать, что всем этим группам соответствует один и тот же параметр.
Характеристики биномиального распределения вычислены ранее:
M (Y ) = np , D (Y ) = np (1- p ).
В разделе "События и вероятности" для биномиальной случайной величины доказан закон больших чисел:
![]()
для любого . С помощью центральной предельной теоремы закон больших чисел можно уточнить, указав, насколько Y / n отличается от р .
Теорема Муавра-Лапласа. Для любых чисел a и b , a < b , имеем

где Ф (х ) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Для доказательства достаточно воспользоваться представлением Y в виде суммы независимых случайных величин, соответствующих исходам отдельных испытаний, формулами для M (Y ) и D (Y ) и центральной предельной теоремой.
Эта теорема для случая р = ½ доказана английским математиком А.Муавром (1667-1754) в 1730 г. В приведенной выше формулировке она была доказана в 1810 г. французским математиком Пьером Симоном Лапласом (1749 – 1827).
Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объема N по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком А , либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина Y , равная числу объектов, обладающих признаком А в случайной выборке объема n , где n < N . Например, число Y дефектных единиц продукции в случайной выборке объема n из партии объема N имеет гипергеометрическое распределение, если n < N . Другой пример – лотерея. Пусть признак А билета – это признак «быть выигрышным». Пусть всего билетов N , а некоторое лицо приобрело n из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.
Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид
 (20)
(20)
где D – число объектов, обладающих признаком А , в рассматриваемой совокупности объема N . При этом y принимает значения от max{0, n - (N - D )} до min{n , D }, при прочих y вероятность в формуле (20) равна 0. Таким образом, гипергеометрическое распределение определяется тремя параметрами – объемом генеральной совокупности N , числом объектов D в ней, обладающих рассматриваемым признаком А , и объемом выборки n .
Простой случайной выборкой объема n из совокупности объема N называется выборка, полученная в результате случайного отбора, при котором любой из наборов из n объектов имеет одну и ту же вероятность быть отобранным. Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативно-технических документах. Один из методов отбора таков: объекты отбирают один из другим, причем на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины «случайная выборка», «случайная выборка без возвращения».
Поскольку объемы генеральной совокупности (партии) N и выборки n обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является D . В статистических методах управления качеством продукции D – обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения D / N – уровень дефектности.
Для гипергеометрического распределения
Последний множитель в выражении для дисперсии близок к 1, если N >10 n . Если при этом сделать замену p = D / N , то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что

при N >10 n , где p = D / N . Справедливо предельное соотношение
и этим предельным соотношением можно пользоваться при N >10 n .
Третье широко используемое дискретное распределение – распределение Пуассона. Случайная величина Y имеет распределение Пуассона, если
![]() ,
,
где λ – параметр распределения Пуассона, и P (Y = y )= 0 для всех прочих y (при y=0 обозначено 0! =1). Для распределения Пуассона
M (Y ) = λ, D (Y ) = λ.
Это распределение названо в честь французского математика С.Д.Пуассона (1781-1840), впервые получившего его в 1837 г. Распределение Пуассона является предельным случаем биномиального распределения, когда вероятность р осуществления события мала, но число испытаний n велико, причем np = λ. Точнее, справедливо предельное соотношение
Поэтому распределение Пуассона (в старой терминологии «закон распределения») часто называют также «законом редких событий».
Распределение Пуассона возникает в теории потоков событий (см. выше). Доказано, что для простейшего потока с постоянной интенсивностью Λ число событий (вызовов), происшедших за время t , имеет распределение Пуассона с параметром λ = Λt . Следовательно, вероятность того, что за время t не произойдет ни одного события, равна e - Λ t , т.е. функция распределения длины промежутка между событиями является экспоненциальной.
Распределение Пуассона используется при анализе результатов выборочных маркетинговых обследований потребителей, расчете оперативных характеристик планов статистического приемочного контроля в случае малых значений приемочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и т.д.
Описание иных параметрических семейств дискретных распределений и возможности их практического использования рассматриваются в литературе.
В некоторых случаях, например, при изучении цен, объемов выпуска или суммарной наработки на отказ в задачах надежности, функции распределения постоянны на некоторых интервалах, в которые значения исследуемых случайных величин не могут попасть.
| Предыдущая |
Мы уже знаем (см. п. 4.1.3), что для полного описания механизма исследуемого случайного эксперимента, т. е. для полного описания вероятностного пространства (или, что то же, для исчерпывающего задания интересующей нас случайной величины), недостаточно задать лишь пространство элементарных событий (и тем самым описать множество теоретически возможных значений анализируемой случайной величины). К этому необходимо добавить также: в дискретном случае - правило сопоставления с каждым возможным значением случайной величины вероятности его появления в непрерывном случае - правило сопоставления с каждой измеримой областью возможных значений случайной величины вероятности события, заключающегося в том, что в случайном эксперименте реализуется одно из возможных значений, принадлежащих заданной области АХ. Это правило, позволяющее устанавливать соответствия вида:

принято называть законом распределения вероятностей исследуемой случайной величины .
Прозрачное пояснение такой терминологии мы получаем в рамках дискретного вероятностного пространства, поскольку в этом случае речь идет о правиле распределения суммарной единичной вероятности (т. е. вероятности достоверного события) между отдельными возможностями
Очевидно, задание закона распределения вероятностей, т. е. соответствий типа (5.2), может осуществляться с помощью таблиц и графиков (только в дискретном случае), а также с помощью функций и алгоритмически (об основных формах задания законов распределения и примерах их модельной, т. е. аналитической, записи см. гл. 6).
Приведем примеры табличного и графического задания законов распределения вероятностей.
Тщательный статистический анализ засоренности партий дефектными изделиями (пример 4.5) позволил построить следующее распределение вероятностей для случайной величины выражающей число дефектных изделий, обнаруженных при контроле партии, состоящей из N=30 изделий, случайно отобранных из продукции массового производства (табл. 5.2):
Таблица 5.2

Значения вероятностей, приведенные в табл. 5.2, даны с точностью до третьего десятичного знака, поэтому то, что суммирование представленных в таблице вероятностей дает 0,998 (вместо единицы), легко объяснимо: недостающие 0,002 как-то «размазаны» между возможными значениями 11, ..., 30, но на каждое отдельное возможное значение приходится вероятность, меньшая 0,0005.
Тот же закон распределения может быть представлен графически (рис. 5.2).
Геометрическое изображение закона распределения вероятностей дискретной случайной величины часто называют полигоном распределения или полигоном частот.
В качестве другого примера рассмотрим фрагмент табл. 5.1, выбрав из одиннадцати представленных в ней компонент только две: качество жилищных условий и среднедушевой доход Еще более упростим рассматриваемую схему, перейдя от по существу непрерывной случайной величины к ее дискретному аналогу отказываясь от точного знания среднедушевого дохода каждой семьи и ограничиваясь лишь тремя возможными градациями: семья имеет низкий доход (градация ), средний доход (градация ) и высокий доход (градация ). С учетом четырех градаций качества жилищных условий: - качество низкое - качество удовлетворительное; - качество хорошее и - качество очень хорошее, и проведенного вероятностно-статистического анализа получаем следующий закон распределения вероятностей двумерной случайной величины (данные условные):
Таблица 5.3

Соответствующий двумерный полигон распределения представлен на рис. 5.3.
Закон распределения вероятностей многомерной случайной величины называют многомерным или совместным. Если каждая из компонент ( см. (5.1)) анализируемого многомерного признака дискретна и имеет конечное число всех возможных значений, то, очевидно, общее число возможных «значений» случайного вектора будет .

Рис. 5.2. Графическое задание закона распределения вероятностей для числа дефектных изделий, обнаруженных в наугад извлеченной партии, состоящей из 30 изделий массового производства

Рис. 5.3. Полигон двумерного распределения семей по качеству жилищных условий и по уровню дохода
В этом случае вместо общей индексации всех возможных многомерных значений удобнее пользоваться -мерной индексацией вида , где первый индекс i определяет номер возможного значения по первой компоненте, второй индекс j - по второй компоненте и т. д. Тогда будет означать возможное значение , полученное сочетанием возможного значения компоненты возможного значения компоненты возможного значения компоненты а вероятности удобно обозначать . Таким образом, в табл. 5.3 представлены вероятности
При анализе многомерных (совместных) распределений часто бывает необходимо получить закон распределения лишь для какой-то части компонент анализируемого векторного признака. Так, многомерная случайная величина , рассмотренная в табл. 5.1, естественно разбивается на два подвектора: описывающий социальнодемографические и экономическую характеристики семьи, и описывающий структуру семейного потребления.
Частный (маржинальный) закон распределения
подвектора анализируемой многомерной случайной величины описывает распределение вероятностей признака в ситуации, когда на значения другой части компонент не накладывается никаких условий. В дискретном случае соответствующие вероятности определяются по формулам: