Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.

Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной .

В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х , общую прямую горизонтальной и профильной плоскостей – осью у , а общую прямую фронтальной и профильной плоскостей – осью z . Точка О , которая принадлежит всем трем плоскостям, называется точкой начала координат.

На рисунке 15а показана точка А и три ее проекции. Проекцию на профильную плоскость (а́́ ) называют профильной проекцией и обозначают а́́ .

Для получения эпюра точки А, которая состоит из трех проекций а, а а , необходимо разрезать трехгранник, образующийся всеми плоскостями, вдоль оси у (рис. 15б) и совместить все эти плоскости с плоскостью фронтальной проекции. Горизонтальную плоскость необходимо вращать около оси х , а профильную плоскость – около оси z в направлении, указанном на рисунке 15 стрелкой.

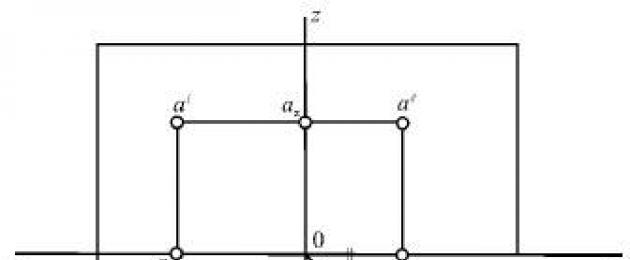
На рисунке 16 изображено положение проекций а, а́ и а́́ точки А , полученное в результате совмещения всех трех плоскостей с плоскостью чертежа.

В результате разреза ось у встречается на эпюре в двух различных местах. На горизонтальной плоскости (рис. 16) она принимает вертикальное положение (перпендикулярно оси х ), а на профильной плоскости – горизонтальное (перпендикулярно оси z ).

На рисунке 16 три проекции а, а́ и а́́ точки А имеют на эпюре строго определенное положение и подчинены однозначным условиям:

а и а́ всегда должны располагаться на одной вертикальной прямой, перпендикулярной оси х ;

а́ и а́́ всегда должны располагаться на одной горизонтальной прямой, перпендикулярной оси z ;

3) при проведении через горизонтальную проекцию а горизонтальной прямой, а через профильную проекцию а́́ – вертикальной прямой построенные прямые обязательно пересекутся на биссектрисе угла между осями проекций, так как фигура Оа у а 0 а н – квадрат.

При выполнении построения трех проекций точки нужно проверять выполняемость всех трех условий для каждой точки.

Координаты точки

Положение точки в пространстве может быть определено с помощью трех чисел, называемых ее координатами . Каждой координате соответствует расстояние точки от какой-нибудь плоскости проекций.

Расстояние определяемой точки А до профильной плоскости является координатой х , при этом х = а˝А (рис. 15), расстояние до фронтальной плоскости – координатой у, причем у = а́А , а расстояние до горизонтальной плоскости – координатой z , при этом z = aA .

На рисунке 15 точка А занимает ширину прямоугольного параллелепипеда, и измерения этого параллелепипеда соответствуют координатам этой точки, т. е., каждая из координат представлена на рисунке 15 четыре раза, т. е.:

х = а˝А = Оа х = а у а = a z á;

y = а́А = Оа y = а x а = а z а˝;

z = aA = Oa z = а x а́ = а y а˝.

На эпюре (рис. 16) координаты х и z встречаются по три раза:

х = а z а ́= Оа x = а y а,

z = а x á = Oa z = а y а˝.

Все отрезки, которые соответствуют координате х (или z ), являются параллельными между собой. Координата у два раза представлена осью, расположенной вертикально:

y = Оа у = а х а

и два раза – расположенной горизонтально:

у = Оа у = а z а˝.

Данное различие появилось из-за того, что ось у присутствует на эпюре в двух различных положениях.

Следует учесть, что положение каждой проекции определяется на эпюре только двумя координатами, а именно:

1) горизонтальной – координатами х и у ,

2) фронтальной – координатами x и z ,

3) профильной – координатами у и z .

Используя координаты х, у и z , можно построить проекции точки на эпюре.

Если точка А задается координатами, их запись определяется так: А (х; у; z ).

При построении проекций точки А нужно проверять выполняемость следующих условий:

1) горизонтальная и фронтальная проекции а и а́ х х ;

2) фронтальная и профильная проекции а́ и а˝ должны располагаться на одном перпендикуляре к оси z , так как имеют общую координату z ;

3) горизонтальная проекция а так же удалена от оси х , как и профильная проекция а удалена от оси z , так как проекции а́ и а˝ имеют общую координату у .

В случае, если точка лежит в любой из плоскостей проекций, то одна из ее координат равна нулю.

Когда точка лежит на оси проекций, две ее координаты равны нулю.

Если точка лежит в начале координат, все три ее координаты равны нулю.

Проекции прямой

Для определения прямой необходимы две точки. Точку определяют две проекции на горизонтальную и фронтальную плоскости, т. е. прямая определяется с помощью проекций двух своих точек на горизонтальной и фронтальной плоскостях.

На рисунке 17 показаны проекции (а и á, b и b́ ) двух точек А и В. С их помощью определяется положение некоторой прямой АВ . При соединении одноименных проекций этих точек (т. е. а и b, а́ и b́ ) можно получить проекции аb и а́b́ прямой АВ.

На рисунке 18 показаны проекции обеих точек, а на рисунке 19 – проекции проходящей через них прямой линии.

Если проекции прямой определяются проекциями двух ее точек, то они обозначаются двумя рядом поставленными латинскими буквами, соответствующими обозначениям проекций точек, взятых на прямой: со штрихами для обозначения фронтальной проекции прямой или без штрихов – для горизонтальной проекции.

Если рассматривать не отдельные точки прямой, а ее проекции в целом, то данные проекции обозначаются цифрами.

Если некоторая точка С лежит на прямой АВ , ее проекции с и с́ находятся на одноименных проекциях прямой ab и а́b́ . Данную ситуацию поясняет рисунок 19.

Следы прямой

След прямой – это точка пересечения ее с некоторой плоскостью или поверхностью (рис. 20).

Горизонтальным следом прямой называется некоторая точка H , в которой прямая встречается с горизонтальной плоскостью, а фронтальным – точка V , в которой данная прямая встречается с фронтальной плоскостью (рис. 20).

На рисунке 21а изображен горизонтальный след прямой, а ее фронтальный след, – на рисунке 21б.

Иногда также рассматривается профильный след прямой, W – точка пересечения прямой с профильной плоскостью.

Горизонтальный след находится в горизонтальной плоскости, т. е. его горизонтальная проекция h совпадает с этим следом, а фронтальная h́ лежит на оси х. Фронтальный след лежит во фронтальной плоскости, поэтому его фронтальная проекция ν́ совпадает с ним же, а горизонтальная v лежит на оси х.

Итак, H = h , и V = ν́. Следовательно, для обозначения следов прямой можно применять буквы h и ν́.

Различные положения прямой

Прямую называют прямой общего положения , если она не параллельна и не перпендикулярна ни одной плоскости проекций. Проекции прямой общего положения тоже не параллельны и не перпендикулярны осям проекций.

Прямые, которые параллельны одной из плоскостей проекций (перпендикулярны одной из осей). На рисунке 22 показана прямая, которая параллельна горизонтальной плоскости (перпендикулярная оси z), – горизонтальная прямая; на рисунке 23 показана прямая, которая параллельна фронтальной плоскости (перпендикулярна оси у ), – фронтальная прямая; на рисунке 24 показана прямая, которая параллельна профильной плоскости (перпендикулярна оси х ), – профильная прямая. Несмотря на то что каждая из данных прямых образует с одной из осей прямой угол, они не пересекают ее, а только скрещиваются с нею.

Из-за того что горизонтальная прямая (рис. 22) параллельна горизонтальной плоскости, ее фронтальная и профильная проекции будут параллельны осям, определяющим горизонтальную плоскость, т. е. осям х и у . Поэтому проекции áb́ || х и a˝b˝ || у z . Горизонтальная проекция ab может занимать любое положение на эпюре.

У фронтальной прямой (рис. 23) проекции аb || x и a˝b˝ || z , т. е. они перпендикулярны оси у , а потому в этом случае фронтальная проекция а́b́ прямой может занимать произвольное положение.

У профильной прямой (рис. 24) аb || у, а́b || z , и обе они перпендикулярны оси х. Проекция а˝b˝ может располагаться на эпюре любым образом.

При рассмотрении той плоскости, которая проецирует горизонтальную прямую на фронтальную плоскость (рис. 22), можно заметить, что она проецирует эту прямую и на профильную плоскость, т. е. она является плоскостью, которая проецирует прямую сразу на две плоскости проекций – фронтальную и профильную. Исходя из этого ее называют дважды проецирующей плоскостью . Таким же образом для фронтальной прямой (рис. 23) дважды проецирующая плоскость проецирует ее на плоскости горизонтальной и профильной проекций, а для профильной (рис. 23) – на плоскости горизонтальной и фронтальной проекций.

Две проекции не могут определить прямую. Две проекции 1 и 1́ профильной прямой (рис. 25) без уточнения на них проекций двух точек этой прямой не определят положения данной прямой в пространстве.

В плоскости, которая перпендикулярна двум заданным плоскостям симметрии, возможно существование бесчисленного множество прямых, для которых данные на эпюре 1 и 1́ являются их проекциями.

Если точка находится на прямой, то ее проекции во всех случаях лежат на одноименных проекциях этой прямой. Обратное положение не всегда справедливо для профильной прямой. На ее проекциях можно произвольным образом указать проекции определенной точки и не быть уверенным в том, что эта точка лежит на данной прямой.

Во всех трех частных случаях (рис. 22, 23 и 24) положения прямой по отношению к плоскости проекций произвольный ее отрезок АВ , взятый на каждой из прямых, проецируется на одну из плоскостей проекций без искажения, т. е. на ту плоскость, которой он параллелен. Отрезок АВ горизонтальной прямой (рис. 22) дает проекцию в натуральную величину на горизонтальную плоскость (аb = АВ ); отрезок АВ фронтальной прямой (рис. 23) – в натуральную величину на плоскость фронтальной плоскости V (áb́ = AB ) и отрезок АВ профильной прямой (рис. 24) – в натуральную величину на профильную плоскость W (a˝b˝ = АВ), т. е. представляется возможным измерить на чертеже натуральную величину отрезка.

Иначе говоря, с помощью эпюр можно определить натуральные размеры углов, которые рассматриваемая прямая образует с плоскостями проекций.

Угол, который составляет прямая с горизонтальной плос костью Н , принято обозначать буквой α, с фронтальной плоскостью – буквой β, с профильной плоскостью – буквой γ.

Любая из рассматриваемых прямых не имеет следа на параллельной ей плоскости, т. е. горизонтальная прямая не имеет горизонтального следа (рис. 22), фронтальная прямая не имеет фронтального следа (рис. 23), а профильная прямая – профильного следа (рис. 24).

Проецирование точки на три плоскости проекций координатного угла начинают с получения ее изображения на плоскости H - горизонтальной плоскости проекций. Для этого через точку А (рис. 4.12, а) проводят проецирующий луч перпендикулярно плоскости H.

На рисунке перпендикуляр к плоскости Н параллелен оси Oz. Точку пересечения луча с плоскостью Н (точку а) выбирают произ­вольно. Отрезок Аа определяет, на каком расстоянии находится точка А от плоскости Н, указывая тем самым однозначно положение точки А на рисунке по отношению к плоскостям проекций. Точка а является прямоугольной проекцией точки А на плоскость Н и называется горизонтальной проекцией точки А (рис. 4.12, а).

Для получения изображения точки А на плоскости V (рис. 4.12,б) через точку А проводят проецирующий луч перпендикулярно фронтальной плоскости проекций V. На рисунке перпендикуляр к плоскости V параллелен оси Оу. На плоскости Н расстояние от точки А до плоскости V изобразится отрезком аа х, параллельным оси Оу и перпендикулярным оси Ох. Если представить себе, что проецирующий луч и его изображение проводят одновременно в направлении плоскости V, то когда изображение луча пересечет ось Ох в точке а х, луч пересечет плоскость V в точке а". Проведя из точки а х в плоскости V перпендикуляр к оси Ох, который является изображением проецирующего луча Аа на плоскости V, в пересечении с проецирующим лучом получают точку а". Точка а" является фронтальной проекцией точки А, т. е. ее изображением на плоскости V.

Изображение точки А на профильной плоскости проекций (рис. 4.12, в) строят с помощью проецирующего луча, перпендикулярного плоскости W. На рисунке перпендикуляр к плоскости W параллелен оси Ох. Проецирующий луч от точки А до плоскости W на плоскости Н изобразится отрезком аа у, параллельным оси Ох и перпендикулярным оси Оу. Из точки Оу параллельно оси Oz и перпендикулярно оси Оу строят изображение проецирующего луча аА и в пересечении с проецирующим лучом получают точку а". Точка а" является профильной проекцией точки А, т. е. изображением точки А на плоскости W.

Точку а" можно построить, проведя от точки а" отрезок а"а z (изображение проецирующего луча Аа" на плоскости V) параллельно оси Ох, а от точки а z - отрезок а"а z параллельно оси Оу до пересечения с проецирующим лучом.

Получив три проекции точки А на плоскостях проекций, координатный угол развертывают в одну плоскость, как показано на рис. 4.11,б, вместе с проекциями точки А и проецирующих лучей, а точку А и проецирующие лучи Аа, Аа" и Аа" убирают. Края совмещенных плоскостей проекций не проводят, а проводят только оси проекций Oz, Оу и Ох, Оу 1 (рис. 4.13).

Анализ ортогонального чертежа точки показывает, что три расстояния - Аа", Аа и Аа" (рис. 4.12, в), характеризующие положение точки А в пространстве, можно определить, отбросив сам объект проецирования - точку А, на развернутом в одну плоскость координатном угле (рис. 4.13). Отрезки а"а z , аа y и Оа х равны Аа" как противоположные стороны соответствующих прямоугольников (рис. 4.12,в и 4.13). Они определяют расстояние, на котором находится точка А от профильной плоскости проекций. Отрезки а"а х, а"а у1 и Оа у равны отрезку Аа, определяют расстояние от точки А до горизонтальной плоскости проекций, отрезки аа х, а"а z и Оа y 1 равны отрезку Аа", определяющему расстояние от точки А до фронтальной плоскости проекций.

Отрезки Оа х, Оа у и Оа z , расположенные на осях проекций, являются графическим выражением размеров координат X, Y и Z точки А. Координаты точки обозначают с индексом соответствующей буквы. Измерив величину этих отрезков, можно определить положение точки в пространстве, т. е. задать координаты точки.

На эпюре отрезки а"а х и аа х располагаются как одна линия, перпендикулярная к оси Ох а отрезки а"а z и a"a z - к оси Оz. Эти лини называются линиями проекционной связи. Они пересекают оси проекций в точках а х и а z соответственно. Линия проекционной связи, соединяющая горизонтальную проекцию точки А с профильной, оказалась «разрезанной» в точке а у.

Две проекции одной и той же точки всегда располагаются на одной линии проекционной связи, перпендикулярной к оси проекций.

Для представления положения точки в пространстве достаточно двух ее проекций и заданного начала координат (точка О) На рис. 4.14, б две проекции точки полностью определяют ее положение в пространстве По этим двум проекциям можно построит профильную проекцию точки А. Поэтому в дальнейшем, если не будет необходимости в профильной проекции, эпюры будут построены на двух плоскостях проекций: V и Н.

Рис. 4.14. Рис. 4.15.

Рассмотрим несколько примеров построения и чтения чертежа точки.

Пример 1. Определение координат точки J заданной на эпюре двумя проекциях (рис. 4.14). Измеряются три отрезка: отрезок Ов Х (координата X), отрезок b Х b (координата Y) и отрезок b Х b" (координата Z). Координаты записывают в следующем п рядке: X, Y и Z, после буквенного обозначения точки, например, В20; 30; 15.

Пример 2 . Построение точки по заданным координатам. Точка С задана координатами С30; 10; 40. На оси Ох (рис. 4.15) находят точку с х, в которой линия проекционной связи пересекает ось проекций. Для этого по оси Ох от начала координат (точка О) откладывают координату X (размер 30) и получают точку с х. Через эту точку перпендикулярно оси Ох проводят линию проекционной связи и от точки вниз откладывают координату У (размер 10), получают точку с - горизонтальную проекцию точки С. Вверх от точки с х по линии проекционной связи откладывают координату Z (размер 40), получают точку с" - фронтальную проекцию точки С.

Пример 3 . Построение профильной проекции точки по заданным проекциям. Заданы проекции точки D - d и d". Через точку О проводят оси проекций Oz, Oy и Оу 1 (рис. 4.16, а). Для построения профильной проекции точки D отточки d" проводят линию проекционной связи, перпендикулярную оси Oz, и продолжают ее вправо за ось Oz. На этой линии будет располагаться профильная проекция точки D. Она будет находиться на таком расстоянии от оси Oz, на каком горизонтальная проекция точки d располагается: от оси Ох, т. е. на расстоянии dd x . Отрезки d z d" и dd x одинаковы, так как определяют одно и то же расстояние - расстояние от точки D до фронтальной плоскости проекций. Это расстояние является координатой У точки D.

Графически отрезок d z d" строят перенесением отрезка dd x с горизонтальной плоскости проекций на профильную. Для этого проводят линию проекционной связи параллельно оси Ох, получают на оси Оу точку d y (рис. 4.16,б). Затем переносят размер отрезка Od y на ось Оу 1 , проведя из точки О дугу радиусом, равным отрезку Od y , до пересечения с осью Оу 1 (рис. 4.16,б), получают точку dy 1 . Эту точку можно построить и как показано на рис. 4.16, в, проведя прямую под углом 45° к оси Оу из точки d y . Из точки d y1 проводят линию проекционной связи параллельно оси Oz и на ней откладывают отрезок, равный отрезку d"d x , получают точку d".

Перенос величины отрезка d x d на профильную плоскость проекций можно осуществить с помощью постоянной прямой чертежа (рис. 4.16, г). В этом случае линию проекционной связи dd y проводят через горизонтальную проекцию точки параллельно оси Оу 1 до пересечения с постоянной прямой, а затем параллельно оси Оу до пересечения с продолжением линии проекционной связи d"d z .

Частные случаи расположения точек относительно плоскостей проекций

Положение точки относительно плоскости проекций определяется соответствующей координатой, т. е. величиной отрезка линии проекционной связи от оси Ох до соответствующей проекции. На рис. 4.17 координата У точки А определяется отрезком аа х - расстояние от точки А до плоскости V. Координата Z точки А определяется отрезком а"а х - расстояние от точки А до плоскости Н. Если одна из координат равна нулю, то точка расположена на плоскости проекций. На рис. 4.17 приведены примеры различного расположения точек относительно плоскостей проекций. Координата Z точки В равна нулю, точка находится в плоскости Н. Ее фронтальная проекция находится на оси Ох и совпадает с точкой b х. Координата У точки С равна нулю, точка располагается на плоскости V, ее горизонтальная проекция с находится на оси Ох и совпадает с точкой с х.

Следовательно, если точка находится на плоскости проекций, то одна из проекций этой точки лежит на оси проекций.

На рис. 4.17 координаты Z и Y точки D равны нулю, следовательно, точка D находится на оси проекций Ох и две ее проекции совпадают.

Глава 6. ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ

§ 32. Комплексный чертеж точки

Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д

Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.

Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П 1 . Проекции элементов

пространства на ней будем обозначать с индексом 1: А 1 , а 1 , S 1 ... и называть горизонтальными проекциями (точки, прямой, плоскости).

Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П 2 . Проекции элементов пространства на ней будем обозначать с индексом 2: А 2 , 2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.

Спроецируем точку А ортогонально на обе плоскости проекций:

АА 1 _|_ П 1 ;AА 1 ^П 1 =A 1 ;

АА 2 _|_ П 2 ;AА 2 ^П 2 =A 2 ;

Проецирующие лучи АА 1 и АА 2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА 1 АА 2 , перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.

Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П 1 с фронтальной плоскостью П 2 вращением вокруг оси П 2 /П 1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П 2 /П 1 . Прямая А 1 А 2 , соединяющая горизонтальную А 1 и фронтальную А 2 проекции точки, называется вертикальной линией связи.

Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.

Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА 1 =h) и глубиной f(AA 2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А 2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f . Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.

60.gif

Изображение:

61.gif

Изображение:

7. Вопросы для самопроверки

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

4. Как называется расстояние, определяющее положение точки относительно плоскости проекций П 1 , П 2 ?

7. Как построить дополнительную проекцию точки на плоскости П 4 _|_ П 2 , П 4 _|_ П 1 , П 5 _|_ П 4 ?

9. Как можно построить комплексный чертеж точки по ее координатам?

33. Элементы трехпроекционного комплексного чертежа точки

§ 33. Элементы трехпроекционного комплексного чертежа точки

Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П 1 и фронтальной плоскости проекций П 2 (рис. 62, а). В результате пересечения фронтальной П 2 и профильной П 3 плоскостей проекций получаем новую ось П 2 /П 3 , которая располагается на комплексном чертеже параллельно вертикальной линии связи A 1 A 2 (рис. 62, б). Третья проекция точки А - профильная - оказывается связанной с фронтальной проекцией А 2 новой линией связи, которую называют горизонталь-

Рис. 62

ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A 1 A 2 _|_ А 2 А 1 и А 2 А 3 , _| _ П 2 /П 3 .

Положение точки в пространстве в этом случае характеризуется ее широтой - расстоянием от нее до профильной плоскости проекций П 3 , которое обозначим буквой р.

Полученный комплексный чертеж точки называется трехпроек-ционным.

В трехпроекционном чертеже глубина точки АА 2 проецируется без искажений на плоскости П 1 и П 2 (рис. 62, а). Это обстоятельство позволяет построить третью - фронтальную проекцию точки А по ее горизонтальной А 1 и фронтальной А 2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A 2 A 3 _|_A 2 A 1 . Затем в любом месте на чертеже провести ось проекций П 2 /П 3 _|_ А 2 А 3 , измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П 2 /П 3 . Получим профильную проекцию А 3 точки А.

Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.

Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-

ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).

62.gif

Изображение:

63.gif

Изображение:

34. Положение точки в пространстве трехмерного угла

§ 34. Положение точки в пространстве трехмерного угла

Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:

• точка расположена в пространстве (см. рис. 62). В этом случае она имеет глубину, высоту и широту;
• точка расположена на плоскости проекций П 1 - она не имеет высоты, П 2 - не имеет глубины, Пз - не имеет широты;
• точка расположена на оси проекций, П 2 /П 1 не имеет глубины и высоты, П 2 /П 3 - не имеет глубины и широты и П 1 /П 3 не имеет высоты и широты.

35. Конкурирующие точки

§ 35. Конкурирующие точки

Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П 1 [А 1 == В 1 ]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости

П 2 (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П 3 [А 3 == B 3 ] (рис. 64, в), они называются профильно конкурирующими.

По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих - та, у которой больше глубина, и у профильно конкурирующих - та, у которой больше широта.

64.gif

Изображение:

36. Замена плоскостей проекций

§ 36. Замена плоскостей проекций

Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.

На рис. 65, а показаны точка А и ее проекции - горизонтальная А 1 и фронтальная А 2 . По условиям задачи необходимо произвести замену плоскостей П 2 . Новую плоскость проекции обозначим П 4 и расположим перпендикулярно П 1 . На пересечении плоскостей П 1 и П 4 получим новую ось П 1 /П 4 . Новая проекция точки А 4 будет расположена на линии связи, проходящей через точку А 1 и перпендикулярно оси П 1 /П 4 .

Поскольку новая плоскость П 4 заменяет фронтальную плоскость проекции П 2 , высота точки А изображается одинаково в натуральную величину и на плоскости П 2 , и на плоскости П 4 .

Это обстоятельство позволяет определить положение проекции A 4 , в системе плоскостей П 1 _|_ П 4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-

сти проекции П 2 , отложить ее на новой линии связи от новой оси проекций - и новая проекция точки А 4 будет построена.

Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П 4 _|_ П 2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А 2 А 4 _|_. В этом случае глубина точки одинакова и на плоскости П 1 , и на плоскости П 4 . На этом основании строят А 4 (рис. 66, б) на линии связи А 2 А 4 на таком расстоянии от новой оси П 1 /П 4 на каком А 1 находится от оси П 2 /П 1 .

Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П 5 . Ее располагают перпендикулярно уже введенной плоскости П 4 (рис. 67, а), т. е. П 5 П 4 и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П 1) и откладывают их на новой линии связи А 4 А 5 , от новой оси проекций П 5 /П 4 . В новой системе плоскостей П 4 П 5 получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А 4 и А 5 , связанных линией связи

Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.

Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А , а проекцию а? на фронтальную плоскость называют фронтальной проекцией .

Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С . Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с … Фронтальные проекции обозначают малыми буквами со штрихом вверху а?, b?, с? …

Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций – арабскими цифрами 1, 2… и 1?, 2?…

При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки .

Через перпендикулярные прямые Аа и Аа? проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аа х, а фронтальную плоскость – по прямой а?а х. Прямые аах и а?а х являются перпендикулярными оси пересечения плоскостей. То есть Аааха? является прямоугольником.

При совмещении горизонтальной и фронтальной плоскостей проекции а и а? будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аа х и а?а х не нарушится.

Получаем, что на эпюре проекции а и а? некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.

Две проекции а и а? некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а? к фронтальной плоскости пройдет через точку А , т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.

Рассмотрим прямоугольник Aaa х а? (рис. 5), для которого справедливы следующие утверждения:

1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.

Аа? = аа х;

2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а? от оси пересечения плоскостей, т. е.

Аа = а?а х.

Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.

Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).

Ось пересечения плоскостей делит горизонтальную плоскость на две четверти – переднюю и заднюю, а фронтальную плоскость – на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.

При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости – с верхней частью фронтальной плоскости.

На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В – во второй, точка С – в третьей и точка D – в четвертой.

При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.

Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция – ниже оси пересечения плоскостей.

Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.

В некоторых частных случаях точка (Е ) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.

В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная k? показывает фактическое местонахождение этой точки.

Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.

Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.

Когда точка не лежит на плоскостях проекций, она называется точкой общего положения . В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.

2. Отсутствие оси проекций

Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.

Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.

При построениях на эпюре всегда следует располагать проекции а и а? точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа? .

Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа? ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а? до их пересечения, можно получить точку А . При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.

3. Проекции точки на три плоскости проекций

Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.

Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной .

В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х , общую прямую горизонтальной и профильной плоскостей – осью у , а общую прямую фронтальной и профильной плоскостей – осью z . Точка О , которая принадлежит всем трем плоскостям, называется точкой начала координат.

На рисунке 15а показана точка А и три ее проекции. Проекцию на профильную плоскость (а?? ) называют профильной проекцией и обозначают а?? .

Для получения эпюра точки А, которая состоит из трех проекций а, а а , необходимо разрезать трехгранник, образующийся всеми плоскостями, вдоль оси у (рис. 15б) и совместить все эти плоскости с плоскостью фронтальной проекции. Горизонтальную плоскость необходимо вращать около оси х , а профильную плоскость – около оси z в направлении, указанном на рисунке 15 стрелкой.

На рисунке 16 изображено положение проекций а, а? и а?? точки А , полученное в результате совмещения всех трех плоскостей с плоскостью чертежа.

В результате разреза ось у встречается на эпюре в двух различных местах. На горизонтальной плоскости (рис. 16) она принимает вертикальное положение (перпендикулярно оси х ), а на профильной плоскости – горизонтальное (перпендикулярно оси z ).

На рисунке 16 три проекции а, а? и а?? точки А имеют на эпюре строго определенное положение и подчинены однозначным условиям:

а и а? всегда должны располагаться на одной вертикальной прямой, перпендикулярной оси х ;

а? и а?? всегда должны располагаться на одной горизонтальной прямой, перпендикулярной оси z ;

3) при проведении через горизонтальную проекцию а горизонтальной прямой, а через профильную проекцию а?? – вертикальной прямой построенные прямые обязательно пересекутся на биссектрисе угла между осями проекций, так как фигура Оа у а 0 а н – квадрат.

При выполнении построения трех проекций точки нужно проверять выполняемость всех трех условий для каждой точки.

4. Координаты точки

Положение точки в пространстве может быть определено с помощью трех чисел, называемых ее координатами . Каждой координате соответствует расстояние точки от какой-нибудь плоскости проекций.

Расстояние определяемой точки А до профильной плоскости является координатой х , при этом х = а?А (рис. 15), расстояние до фронтальной плоскости – координатой у, причем у = а?А , а расстояние до горизонтальной плоскости – координатой z , при этом z = aA .

На рисунке 15 точка А занимает ширину прямоугольного параллелепипеда, и измерения этого параллелепипеда соответствуют координатам этой точки, т. е., каждая из координат представлена на рисунке 15 четыре раза, т. е.:

х = а?А = Оа х = а у а = a z a?;

y = а?А = Оа y = а x а = а z а?;

z = aA = Oa z = а x а? = а y а?.

На эпюре (рис. 16) координаты х и z встречаются по три раза:

х = а z а?= Оа x = а y а,

z = а x a? = Oa z = а y а?.

Все отрезки, которые соответствуют координате х (или z ), являются параллельными между собой. Координата у два раза представлена осью, расположенной вертикально:

y = Оа у = а х а

и два раза – расположенной горизонтально:

у = Оа у = а z а?.

Данное различие появилось из-за того, что ось у присутствует на эпюре в двух различных положениях.

Следует учесть, что положение каждой проекции определяется на эпюре только двумя координатами, а именно:

1) горизонтальной – координатами х и у ,

2) фронтальной – координатами x и z ,

3) профильной – координатами у и z .

Используя координаты х, у и z , можно построить проекции точки на эпюре.

Если точка А задается координатами, их запись определяется так: А (х; у; z ).

При построении проекций точки А нужно проверять выполняемость следующих условий:

1) горизонтальная и фронтальная проекции а и а? х х ;

2) фронтальная и профильная проекции а? и а? должны располагаться на одном перпендикуляре к оси z , так как имеют общую координату z ;

3) горизонтальная проекция а так же удалена от оси х , как и профильная проекция а удалена от оси z , так как проекции а? и а? имеют общую координату у .

В случае, если точка лежит в любой из плоскостей проекций, то одна из ее координат равна нулю.

Когда точка лежит на оси проекций, две ее координаты равны нулю.

Если точка лежит в начале координат, все три ее координаты равны нулю.

Точка в пространстве определяется любыми двумя своими проекциями. При необходимости построения третьей проекции по двум заданным необходимо воспользоваться соответствием отрезков линий проекционной связи, полученных при определении расстояний от точки до плоскости проекций (см. рис. 2.27 и рис. 2.28).

Примеры решения задач в I октанте

Дано А 1 ; А 2	Построить А 3
Дано А 2 ; А 3	Построить А 1
Дано А 1 ; А 3	Построить А 2

Рассмотрим алгоритм построения точки А (табл. 2.5)

Таблица 2.5

Алгоритм построения точки А
по заданным координатам А (x = 5, y = 20, z = -9)

В следующих главах мы будем рассматривать образы: прямые и плоскости только в первой четверти. Хотя все рассматриваемые способы можно применить в любой четверти.

Выводы

Таким образом, на основании теории Г. Монжа, можно преобразовать пространственное изображение образа (точки) в плоскостное.

Эта теория основывается на следующих положениях:

1. Все пространство делится на 4 четверти с помощью двух взаимно перпендикулярных плоскостей p 1 и p 2 , либо на 8 октантов при добавлении третьей взаимно-перпендикулярной плоскости p 3 .

2. Изображение пространственного образа на эти плоскости получается с помощью прямоугольного (ортогонального) проецирования.

3. Для преобразования пространственного изображения в плоскостное считают, что плоскость p 2 – неподвижна, а плоскость p 1 вращается вокруг оси x так, что положительная полуплоскость p 1 совмещается с отрицательной полуплоскостью p 2 , отрицательная часть p 1 – с положительной частью p 2 .

4. Плоскость p 3 вращается вокруг оси z (линии пересечения плоскостей) до совмещения с плоскостью p 2 (см. рис. 2.31).

Изображения, получающиеся на плоскостях p 1 , p 2 и p 3 при прямоугольном проецировании образов, называются проекциями.

Плоскости p 1 , p 2 и p 3 вместе с изображенными на них проекциями, образуют плоскостной комплексный чертеж или эпюр.

Линии, соединяющие проекции образа ^ осям x , y , z , называются линиями проекционной связи.

Для более точного определения образов в пространстве может быть применена система трех взаимно перпендикулярных плоскостей p 1 , p 2 , p 3 .

В зависимости от условия задачи можно выбрать для изображения либо систему p 1 , p 2 , либо p 1 , p 2 , p 3 .

Систему плоскостей p 1 , p 2 , p 3 можно соединить с системой декартовых координат, что дает возможность задавать объекты не только графическим или (вербальным) образом, но и аналитическим (с помощью цифр).

Такой способ изображения образов, в частности точки, дает возможность решать такие позиционные задачи, как:

• расположение точки относительно плоскостей проекций (общее положение, принадлежность плоскости, оси);
• положение точки в четвертях (в какой четверти расположена точка);
• положение точек относительно друг друга, (выше, ниже, ближе, дальше относительно плоскостей проекций и зрителя);
• положение проекций точки относительно плоскостей проекций (равноудаление, ближе, дальше).

Метрические задачи:

• равноудаленность проекции от плоскостей проекций;
• отношение удаления проекции от плоскостей проекций (в 2–3 раза, больше, меньше);
• определение расстояния точки от плоскостей проекций (при введении системы координат).

Вопросы для самоанализа

1. Линией пересечения каких плоскостей является ось z ?

2. Линией пересечения каких плоскостей является ось y ?

3. Как располагается линия проекционной связи фронтальной и профильной проекции точки? Покажите.

4. Какими координатами определяется положение проекции точки: горизонтальной, фронтальной, профильной?

5. В какой четверти располагается точка F (10; –40; –20)? От какой плоскости проекций точка F удалена дальше всего?

6. Расстоянием от какой проекции до какой оси определяется удаление точки от плоскости p 1 ? Какой координатой точки является это расстояние?

• Total: 0
• Вконтакте0
• Google+0
• ОК0
• Facebook0