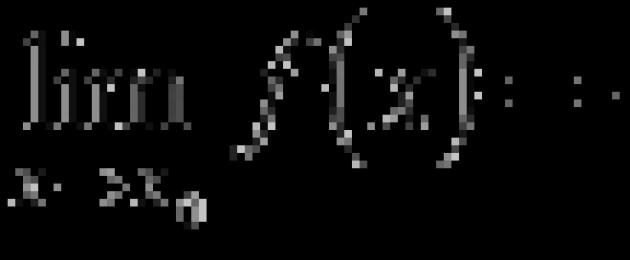Предел по коши. Предел функции в точке и на бесконечности. Эквивалентность определений предела функции по Гейне и по Коши. Геометрический смысл предела. Односторонние пределы. Основные теоремы о пределах функции. а. База; определение и основные примеры

Начнем с общих вещей, которые ОЧЕНЬ важны, но мало кто обращает на них внимание.

Предел функции - основные понятия.

Бесконечность обозначают символом . По сути, бесконечность это есть либо бесконечно большое положительное число , либо бесконечно большое отрицательное число .

Что это означает: когда Вы видите , то не имеет разницы это или . Но лучше не заменять на , равно как и лучше не заменять на .

Записывать предел функции f(x) принято в виде , снизу указывается аргумент x и через стрелочку к какому значению он стремится.

Если представляет из себя конкретное действительное число, то говорят о пределе функции в точке .

Если или . то говорят о пределе функции на бесконечности .

Сам предел может быть равен конкретному действительному числу , в этом случае говорят, что предел конечен .

Если , или , то говорят, что предел бесконечен .

Еще говорят, что предел не существует , если нельзя определить конкретное значение предела или его бесконечное значение (, или ). Например, предел от синуса на бесконечности не существует.

Предел функции - основные определения.

Пришло время заняться нахождением значений пределов функций на бесконечности и в точке. В этом нам помогут несколько определений. Эти определения опираются на числовые последовательности и их сходимость или расходимость .

Определение (нахождение предела функции на бесконечности).

Число А называется пределом функции f(x) при , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А . Обозначается .

Замечание.

Предел функции f(x) при бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается .

Пример.

Используя определение предела при доказать равенство .

Решение.

Запишем последовательность значений функции для бесконечно большой положительной последовательности значений аргумента .

Очевидно, что члены этой последовательности монотонно убывают к нулю.

Графическая иллюстрация.

Теперь запишем последовательность значений функции для бесконечно большой отрицательной последовательности значений аргумента .

Члены этой последовательности также монотонно убывают к нулю, что доказывает исходное равенство.

Графическая иллюстрация.

Пример.

Найти предел

Решение.

Запишем последовательность значений функции для бесконечно большой положительной последовательности значений аргумента. К примеру, возьмем .

Последовательность значений функции при этом будет (синие точки на графике)

Очевидно, что эта последовательность является бесконечно большой положительной, следовательно,

А сейчас запишем последовательность значений функции для бесконечно большой отрицательной последовательности значений аргумента. К примеру, возьмем .

Последовательность значений функции при этом будет (зеленые точки на графике)

Очевидно, что эта последовательность сходится к нулю, следовательно,

Графическая иллюстрация

Ответ:

Сейчас поговорим о существовании и нахождении предела функции в точке. Все основывается на определении односторонних пределов . Без вычисления односторонних пределов не обойтись при .

Определение (нахождение предела функции слева).

Число В называется пределом функции f(x) слева при , если для любой сходящейся к а последовательности аргументов функции , значения которых остаются меньше а (), последовательность значений этой функции сходится к В .

Обозначается .

Определение (нахождение предела функции справа).

Число В называется пределом функции f(x) справа при , если для любой сходящейся к а последовательности аргументов функции , значения которых остаются больше а (), последовательность значений этой функции сходится к В .

Обозначается .

Определение (существование предела функции в точке).

Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.

Замечание.

Предел функции f(x) в точке а бесконечен, если пределы слева и справа а бесконечны.

Поясним эти определения на примере.

Пример.

Доказать существование конечного предела функции в точке . Найти его значение.

Решение.

Будем отталкиваться от определения существования предела функции в точке.

Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов , сходящуюся к , причем . Примером такой последовательности может являться

На рисунке соответствующие значения показаны зелеными точками.

Легко видеть, что эта последовательность сходится к -2 , поэтому .

Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов , сходящуюся к , причем . Примером такой последовательности может являться

Соответствующая последовательность значений функции будет иметь вид

На рисунке соответствующие значения показаны синими точками.

Легко видеть, что эта последовательность также сходится к -2 , поэтому .

Этим мы показали, что пределы слева и справа равны, следовательно, по определению существует предел функции в точке , причем

Графическая иллюстрация.

Продолжить изучение основных определений теории пределов рекомендуем темой .

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности {x n}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству

Записывают это следующим образом: или x n → a.

Неравенство (6.1) равносильно двойному неравенству

a - ε < x n < a + ε которое означает, что точки x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .

Последовательность, имеющая предел, называется сходящейся , в противном случае - расходящейся .

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .

Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.

Определение 2 . Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0 < x-a < ε , значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε

Это определение называют определением предел функции по Коши, или “на языке ε - δ "

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде

В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1 . Если существует каждый предел

(6.4)

(6.5)

(6.6)

Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.

Теорема 2.

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,

Теорема 3.

(6.11)

где e » 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x o , если предел

и непрерывной слева в точке x o, если предел

Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .

2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .

Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода - в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.

Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1| < ε

Возьмем любое ε > 0. Так как x n -1 =(n+1)/n - 1= 1/n, то для отыскания N достаточно решить неравенство 1/n<ε. Отсюда n>1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .

Пример 3.2. Найти предел последовательности, заданной общим членом .

Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:

Пример 3.3 . . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4 . Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.

Пример 3.6 . Доказать, что предел не существует.

Решение. Пусть x 1 , x 2 ,..., x n ,... - последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞

Если x n = p n, то sin x n = sin (p n) = 0 при всех n и предел Если же
x n =2 p n+ p /2, то sin x n = sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Бесконечно малые и бесконечно большие функции. Понятие о неопределенностях. Раскрытие простейших неопределенностей. Первый и второй замечательные пределы. Основные эквивалентности. Функции, эквивалентные функциям в окрестности .

Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.

СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ

Аналитический способ: функция задается с помощью

математической формулы.

Табличный способ: функция задается с помощью таблицы.

Описательный способ: функция задается словесным описанием

Графический способ: функция задается с помощью графика

Пределы на бесконечности

Пределы функции на бесконечности

Элементарные функции:

1) степенная функция y=x n

2) показательная функция y=a x

3) логарифмическая функция y=log a x

4) тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x

5) обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.

ПустьиТогда система множеств

является фильтром и обозначается или Пределназывается пределом функции f при x стремящемся к бесконечности.

Опр.1. (по Коши). Пусть задана функция y=f(x): X à Y и точка a является предельной для множества X. Число A называется пределом функции y=f(x) в точке a , если для любого ε > 0 можно указать такое δ > 0, что для всех xX, удовлетворяющим неравенствам 0 < |x-a | < δ, выполняется |f(x) – A | < ε.

Опр.2.(по Гейне). Число A называется пределом функции y=f(x) в точке a , если для любой последовательности {x n }ε X, x n ≠a nN, сходящийся к a , последовательность значений функции {f(x n)} сходится к числу A .

Теорема . Определение предела функции по Коши и по Гейне эквиваленты.

Доказательство . Пусть A=lim f(x) – предел функции y=f(x) по Коши и {x n } X, x n a nN – последовательность, сходящаяся к a , x n à a .

По данному ε > 0 найдем δ > 0 такое, что при 0 < |x-a | < δ, xX имеем |f(x) – A | < ε, а по этому δ найдем номер n δ =n(δ) такой, что при n>n δ имеем 0 < |x n -a | < δ

Но тогда |f(x n) – A | < ε, т.е. доказано, что f(x n)à A .

Пусть теперь число A есть теперь предел функции по Гейне, но A не является пределом по Коши. Тогда найдется ε o > 0 такое, что для всех nN существуют x n X, 0 < |x n -a| < 1/n, для которых |f(x n)-A| >= ε o . Это означает, что найдена последовательность {x n } X, x n ≠a nN, x n à a такая, что последовательность {f(x n)} не сходится к A .

Геометрический смысл предела lim f (x ) функции в точке х 0 таков: если аргументы х будут взяты в ε-окрестности точки х 0 , то соответствующие значения останутся в ε-окрестности точки.

Функции могут быть заданы на интервалах, примыкающих к точке x0 разными формулами, либо не определены на одном из интервалов. Для исследования поведения таких функций удобным является понятие левосторонних и правосторонних пределов.

Пусть функция f определена на интервале (a, x0). Число A называется пределом функции f слева

в точке x0 если0 0 x (a, x0) , x0 - x x0: | f (x) - A |

Предел функции f справа в точке x0 определяется аналогично.

Бесконечно малые функции обладают следующими свойствами:

1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке.

Бесконечно малые в некоторой точке х0 функции a (x) и b (x) называются бесконечно малыми одного порядка ,

Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям

Элементарными приемами раскрытия неопределенностей являются:

сокращение на множитель, создающий неопределенность

деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при)

применение эквивалентных бесконечно малых и бесконечно больших

использование двух замечательных пределов:

Первый замечательный преде л

Второй замечательный предел

Функции f(x) и g(x) называются эквивалентными при x→ a, если f(x): f(x) = f (x)g(x), где limx→ af (x) = 1.

Иначе говоря функции эквивалентны при x→ a, если предел их отношения при x→ a равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами :

sin x ~ x, x → 0

tg x ~ x, x → 0, arcsin x ~ x, x ® 0, arctg x~ x, x ® 0

e x -1~ x, x→ 0

ln (1+x)~ x, x→ 0

m -1~ mx, x→ 0

Непрерывность функции. Непрерывность элементарных функций. Арифметические операции над непрерывными функциями. Непрерывность сложной функции. Формулировка теорем Больцано-Коши и Вейерштрасса.

Разрывные функции. Классификация точек разрыва. Примеры.

Функция f(x) называется непрерывной в точке a, если

" U(f(a)) $ U(a) (f(U(a))М U(f(a))).

Непрерывность сложной функции

Теорема 2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 59.

Все элементарные функции непрерывны в каждой точке их областей определения.

Теорема Вейерштрасса

Пусть f - непрерывная функция, определённая на отрезке . Тогда для любого существует такой многочлен p с вещественными коэффициентами, что для любого x из выполнено условие

Теорема Больцано - Коши

Пусть дана непрерывная функция на отрезке Пусть такжеи без ограничения общности предположим, чтоТогда для любогосуществуеттакое, что f(c) = C.

Точка разрыва - значение аргумента, при котором нарушается непрерывность функции (см. Непрерывная функция). В простейших случаях нарушение непрерывности в некоторой точке а происходит так, что существуют пределы

при стремлении x к а справа и слева, но хотя бы один из этих пределов отличен от f (a). В этом случае а называют Точкой разрыва 1-го рода . Если при этом f (a + 0) = f (a -0), то разрыв называется устранимым, так как функция f (x) становится непрерывной в точке а, если положить f (a)= f(a+0)=f(a-0).

Разрывные функции, функции, имеющие разрыв в некоторых точках (см. Разрыва точка). Обычно у функций, встречающихся в математике, точки разрыва изолированы, но существуют функции, для которых все точки являются точками разрыва, например функция Дирихле: f (x) = 0, если х рационально, и f (x) = 1, если х иррационально. Предел всюду сходящейся последовательности непрерывных функций может быть Р. ф. Такие Р. ф. называются функциями первого класса по Бэру.

Производная, ее геометрический и физический смысл. Правила дифференцирования (производная суммы, произведения, частного двух функций; производная сложной функции).

Производная тригонометрических функций.

Производная обратной функции. Производная обратных тригонометрических функций.

Производная логарифмической функции.

Понятие о логарифмическом дифференцировании. Производная степенно-показательной функции. Производная степенной функции. Производная показательной функции. Производная гиперболических функций.

Производная функции, заданной параметрически.

Производная неявной функции.

Производной функции f(x) (f"(x0)) в точке x0 называется число, к которому стремится разностное отношение , стремящемся к нулю.

Геометрический смысл производной . Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.

Уравнение касательной к графику функции y=f(x) в точке x0:

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

Логарифмическое дифференцирование

Если требуется найти из уравнения, то можно:

а) логарифмировать обе части уравнения

б) дифференцировать обе части полученного равенства, где есть сложная функция от х,

.

в) заменить его выражением через х

Дифференцирование неявных функций

Пусть уравнение определяеткак неявную функцию от х.

а) продифференцируем по х обе части уравнения , получим уравнение первой степени относительно;

б) из полученного уравнения выразим .

Дифференцирование функций, заданных параметрически

Пусть функция задана параметрическими уравнениями ,

Тогда , или

Дифференциал. Геометрический смысл дифференциала. Применение дифференциала в приближенных вычислениях. Инвариантность формы первого дифференциала. Критерий дифференцируемости функции.

Производные и дифференциалы высших порядков.

Дифференциал (от лат. differentia - разность, различие) в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0 производную, то приращение Dy = f (x0 + Dx) - f (x0) функции f (x) можно представить в виде Dy = f" (x0) Dx + R,

где член R бесконечно мал по сравнению с Dх. Первый член dy = f" (x0) Dх в этом разложении и называется дифференциалом функции f (x) в точке x0.

ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f"(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f"(x) , а dx=Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.

Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2 y: d(dy)=d 2 y.

Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому

d 2 y = d(dy) = d = "dx = f ""(x)dx·dx = f ""(x)(dx) 2 .

Принято записывать (dx) 2 = dx 2 . Итак, d 2 у= f""(x)dx 2 .

Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:

d 3 y=d(d 2 y)="dx=f """(x)dx 3 .

Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: d n (y)=d(d n -1y)d n y = f (n)(x)dx n

Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ

Пусть нам известно значение функции y0=f(x0) и ее производной y0" = f "(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δy можно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dy или Δy≈f"(x0)·Δx.

Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f"(x0)·Δx.

Откуда f(x) ≈ f(x0) + f"(x0)·Δx

Инвариантная форма первого дифференциала.

Доказательство:

1)

Основные теоремы о дифференцируемых функциях. Связь между непрерывностью и дифференцируемостью функции. Теорема Ферма. Теоремы Ролля, Лагранжа, Коши и их следствия. Геометрический смысл теорем Ферма, Ролля и Лагранжа.

Доказывая свойства предела функции, мы убедились, что от проколотых окрестностей, в которых были определены наши функции и которые возникали в процессе доказательств, кроме свойств указанных во введении к предыдущему пункту 2, действительно ничего не потребовалось. Это обстоятельство служит оправданием для выделения следующего математического объекта.

а. База; определение и основные примеры

Определение 11. Совокупность В подмножеств множества X будем называть базой в множестве X, если выполнены два условия:

Иными словами, элементы совокупности В суть непустые множества и в пересечении любых двух из них содержится некоторый элемент из той же совокупности.

Укажем некоторые наиболее употребительные в анализе базы.

Если то вместо пишут и говорят, что х стремится к а справа или со стороны больших значений (соответственно, слева или со стороны меньших значений). При принята краткая запись вместо

Запись будет употребляться вместо Она означает, что а; стремится по множеству Е к а, оставаясь больше (меньше), чем а.

то вместо пишут и говорят, что х стремится к плюс бесконечности (соответственно, к минус бесконечности).

Запись будет употребляться вместо

При вместо мы (если это не ведет к недоразумению) будем, как это принято в теории предела последовательности, писать

Заметим, что все перечисленные базы обладают той особенностью, что пересечение любых двух элементов базы само является элементом этой базы, а не только содержит некоторый элемент базы. С другими базами мы встретимся при изучении функций, заданных не на числовой оси.

Отметим также, что используемый здесь термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра», а введенный ниже предел по базе есть наиболее существенная для анализа часть созданного современным французским математиком А. Картаном понятия предела по фильтру

b. Предел функции по базе

Определение 12. Пусть - функция на множестве X; В - база в X. Число называется пределом функции по базе В, если для любой окрестности точки А найдется элемент базы, образ которого содержится в окрестности

Если А - предел функции по базе В, то пишут

Повторим определение предела по базе в логической символике:

Поскольку мы сейчас рассматриваем функции с числовыми значениями, полезно иметь в виду и следующую форму этого основного определения:

В этой формулировке вместо произвольной окрестности V (А) берется симметричная (относительно точки А) окрестность (е-окрестность). Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).

Мы дали общее определение предела функции по базе. Выше были рассмотрены примеры наиболее употребительных в анализе баз. В конкретной задаче, где появляется та или иная из этих баз, необходимо уметь расшифровать общее определение и записать его для конкретной базы.

Рассматривая примеры баз, мы, в частности, ввели понятие окрестности бесконечности. Если использовать это понятие, то в соответствии с общим определением предела разумно принять следующие соглашения:

или, что то же самое,

Обычно под подразумевают малую величину. В приведенных определениях это, разумеется, не так. В соответствии с принятыми соглашениями, например, можем записать

Для того чтобы можно было считать доказанными и в общем случае предела по произвольной базе все те теоремы о пределах, которые мы доказали в пункте 2 для специальной базы , необходимо дать соответствующие определения: финально постоянной, финально ограниченной и бесконечно малой при данной базе функций.

Определение 13. Функция называется финально постоянной при базе В, если существуют число и такой элемент базы, в любой точке которого

Определение 14. Функция называется ограниченной при базе В или финально ограниченной при базе В, если существуют число с и такой элемент базы, в любой точке которого

Определение 15. Функция называется бесконечно малой при базе В, если

После этих определений и основного наблюдения о том, что для доказательства теорем о пределах нужны только свойства базы, можно считать, что все свойства предела, установленные в пункте 2, справедливы для пределов по любой базе.

В частности, мы можем теперь говорить о пределе функции при или при или при

Кроме того, мы обеспечили себе возможность применения теории пределов и в том случае, когда функции будут определены не на числовых множествах; в дальнейшем это окажется особенно ценным. К примеру, длина кривой есть числовая функция, определенная на некотором классе кривых. Если мы знаем эту функцию на ломаных, то потом предельным переходом определяем ее для более сложных кривых, например для окружности.

В данный же момент основная польза от сделанного наблюдения и введенного в связи с ним понятия базы состоит в том, что они избавляют нас от проверок и формальных доказательств теорем о пределах для каждого конкретного вида предельных переходов или, в нашей нынешней терминологии, для каждого конкретного вида баз.

Для того чтобы окончательно освоиться с понятием предела по произвольной базе, доказательства дальнейших свойств предела функции мы проведем в общем виде.

Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции , а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна . И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций , в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей , на котором я фактически уже сформулировал строгое определение.

Какие значки помимо знаков неравенств и модуля вы знаете?

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что» , в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние , т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

И в самом деле, немного порассуждаем – как сформулировать строгое определение последовательности? …Первое, что приходит на ум в свете практического занятия : «предел последовательности – это число, к которому бесконечно близко приближаются члены последовательности».

Хорошо, распишем последовательность :

Нетрудно уловить, что подпоследовательность бесконечно близко приближаются к числу –1, а члены с чётными номерами – к «единице».

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный .

Примечание : у последовательности нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.

Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде (чем я не совсем корректно пользовался в упрощённых объяснениях практических примеров) , но сейчас нам нужно отыскать строгое определение.

Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка» вообще принимает два фиксированных значения.

Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил известный маэстро , который, по существу, и оформил классический матанализ во всей его строгости. Коши предложил оперировать окрестностями , чем значительно продвинул теорию.

Рассмотрим некоторую точку и её произвольную -окрестность:

Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно . Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности . Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками и должно быть меньше «эпсилон»: . Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак модуля : .

Определение : число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами окажутся внутри окрестности:

Или короче: , если

Иными словами, какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.

Так, например, «бесконечный хвост» последовательности ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую -окрестность точки . Таким образом, это значение является пределом последовательности по определению. Напоминаю, что последовательность, предел которой равен нулю, называют бесконечно малой .

Следует отметить, что для последовательности уже нельзя сказать «бесконечный хвост зайдёт » – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.

Теперь покажем, что у последовательности не существует предела. Рассмотрим, например, окрестность точки . Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус единице». По аналогичной причине не существует предела и в точке .

Закрепим материал практикой:

Пример 1

Доказать что предел последовательности равен нулю. Указать номер , после которого, все члены последовательности гарантированно окажутся внутри любой сколь угодно малой -окрестности точки .

Примечание : у многих последовательностей искомый натуральный номер зависит от значения – отсюда и обозначение .

Решение : рассмотрим произвольную найдётся ли номер – такой, что ВСЕ члены с бОльшими номерами окажутся внутри этой окрестности:

Чтобы показать существование искомого номера , выразим через .

Так как при любом значении «эн» , то знак модуля можно убрать:

Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции . При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:

Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:

Примечание : иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.

А теперь смотрим на неравенство и вспоминаем, что изначально мы рассматривали произвольную -окрестность, т.е. «эпсилон» может быть равно любому положительному числу.

Вывод : для любой сколько угодно малой -окрестности точки нашлось значение . Таким образом, число является пределом последовательности по определению. Что и требовалось доказать .

К слову, из полученного результата хорошо просматривается естественная закономерность: чем меньше -окрестность – тем больше номер , после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.

Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.

Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:

Пример 2

Решение : по определению последовательности нужно доказать, что (проговариваем вслух!!!) .

Рассмотрим произвольную -окрестность точки и проверим, существует ли натуральный номер – такой, что для всех бОльших номеров выполнено неравенство:

Чтобы показать существование такого , нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:

Модуль уничтожает знак «минус»:

Знаменатель положителен при любом «эн», следовательно, палки можно убрать:

Перетасовка:

Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при некоторых «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:

Почему так можно сделать? Если, условно говоря, окажется, что , то подавно будет выполнено и условие . Модуль может только увеличить разыскиваемый номер , и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в -окрестности. Кстати, именно поэтому нам не страшнО финальное округление правой части в бОльшую сторону.

Извлекаем корень:

И округляем результат:

Вывод : т.к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что для всех бОльших номеров выполнено неравенство . Таким образом, по определению. Что и требовалось доказать .

Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство ни в коем случае нельзя ослаблять , вычитая, скажем, единицу:

Опять же условно: если номер точно подойдёт, то предыдущий может уже и не подойти.

Следующий пример для самостоятельного решения:

Пример 3

Используя определение последовательности, доказать, что

Краткое решение и ответ в конце урока.

Если последовательность бесконечно велика , то определение предела формулируется похожим образом: точка называется пределом последовательности, если для любого, сколь угодно большого числа существует номер , такой, что для всех бОльших номеров , будет выполнено неравенство . Число называют окрестностью точки «плюс бесконечность» :

Иными словами, какое бы большое значение мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в -окрестность точки , оставив слева лишь конечное число членов.

Дежурный пример:

И сокращённая запись: , если

Для случая запишите определение самостоятельно. Правильная версия в конце урока.

После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно) . Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.

Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!

Строгое определение предела функции

Начнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции формулируется значительно проще: «число является пределом функции , если при «икс», стремящемся к (и слева, и справа) , соответствующие значения функции стремятся к » (см. чертёж) . Всё вроде бы нормально, но слова словами, смысл смыслом, значок значком, а строгих математических обозначений маловато. И во втором параграфе мы познакомимся с двумя подходами к решению данного вопроса.

Пусть функция определена на некотором промежутке за исключением, возможно, точки . В учебной литературе общепринято считают, что функция там не определена:

Такой выбор подчёркивает суть предела функции : «икс» бесконечно близко приближается к , и соответствующие значения функции – бесконечно близко к . Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение , при этом не важно – определена ли функция в точке или нет.

Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.

Рассмотрим последовательность точек (на чертеже отсутствуют) , принадлежащих промежутку и отличных от , которая сходится к . Тогда соответствующие значения функции тоже образуют числовую последовательность, члены которой располагаются на оси ординат.

Предел функции по Гейне для любой последовательности точек (принадлежащих и отличных от ) , которая сходится к точке , соответствующая последовательность значений функции сходится к .

Эдуард Гейне – это немецкий математик. …И не надо тут ничего такого думать, гей в Европе всего лишь один – это Гей-Люссак =)

Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность) . По мотивам предыдущего параграфа, запись означает, что некоторое значение функции находится внутри «эпсилон»-окрестности.

Теперь найдём -окрестность, которая соответствует заданной -окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз) . Обратите внимание, что значение выбирается по длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши : число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой) , существует -окрестность точки , ТАКАЯ , что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки) .

Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая -окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание : если вам потребуется сформулировать только определение по Гейне или только определение по Коши , пожалуйста, не забывайте о существенном предварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки » . Я обозначил это единожды в самом начале и каждый раз не повторял.

Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!) , который также называют «предел на языке »:

Пример 4

Используя определение предела, доказать, что

Решение : функция определена на всей числовой прямой кроме точки . Используя определение , докажем существование предела в данной точке.

Примечание : величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение

Рассмотрим произвольную -окрестность. Задача состоит в том, чтобы по этому значению проверить, существует ли -окрестность, ТАКАЯ , что из неравенства следует неравенство .

Предполагая, что , преобразуем последнее неравенство:
(разложили квадратный трёхчлен )