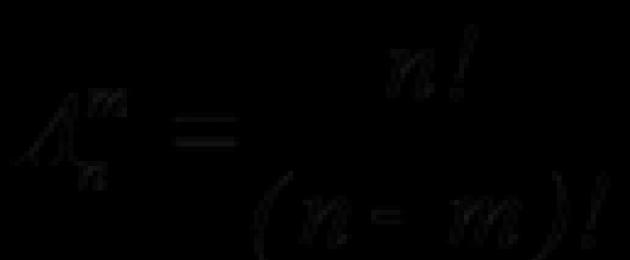Сочетания без повторений. Перестановки, размещения и сочетания. Формулы. Размещения без повторений из $n$ элементов по $k$

Основные формулы комбинаторики

Задачи, в которых речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами . Область математики, в которой рассматриваются комбинаторные задачи, называют комбинаторикой .

Комбинаторика – область математики, в которой рассматриваются задачи о тех или иных комбинациях объектов.

Правило суммы

Пусть имеется n попарно непересекающихся множеств A 1 , A 2 ,…A n, содержащих m 1 , m 2 ,…, m n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно

m 1 m 2 … m n .

Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из них можно выбрать одного студента?

Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно сложить все эти способы:

25 30 20=75.

Ответ: выбрать одного студента из трех групп можно 75 способами.

Правило произведения

Пусть имеется. n множеств A 1 , A 2 ,…A n ,содержащих m 1 , m 2,…, m n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества

m 1 ּm 2 ּ …ּm n .

Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из каждой из них можно выбрать по одному студенту?

Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно перемножить эти числа:

25ּ30ּ20=15000.

Ответ: для того, чтобы из каждой группы выбрать по одному студенту, существует 15000 способов.

^ Если выбираем один элемент из нескольких множеств, то применяем правило суммы.

Если выбираем по одному элементу из нескольких множеств, то применяем правило произведения.

Факториалом числаn называется последовательное произведение натуральных чисел от единицы до самого числа n:

Примечание: 0!=1.

Перестановки без повторений

Перестановками из n различных элементов называются размещения из этих n элементов по n. Перестановки - частный случай размещений.

Пример. Сколькими способами можно расставить в шеренгу студентов группы из 25 человек?

Решение. Число способов есть число перестановок из 25 элементов, то есть:

P 25 = 25ּ24ּ23ּ…ּ1=25!=1,55ּ10 25 .

Ответ: расставить в шеренгу студентов группы из 25 человек можно 1,55ּ10 25 способами.

Размещения без повторений

Различные упорядоченные подмножества по m элементов данного множества, содержащего n элементов, называются размещениями из n по m. Их число равно:

В частности: .

Пример. Из группы, состоящей из 25 человек, надо выбрать шахматную команду из четырех человек на I, II, III и IV доски. Сколькими способами это можно сделать?

Решение. Так как из 25 человек выбираются 4 и порядок важен, то число способов есть число размещений из 25 по 4, то есть:

Ответ: выбрать из 25 человек шахматную команду из четырех человек на I, II, III и IV доски можно 303600 способами.

Сочетания без повторений.

Различные неупорядоченные подмножества по m элементов из данного множества, содержащего n элементов, называются сочетаниями из n по m. Их число равно:

В частности, .

Пример. Сколькими способами из группы в 25 человек можно выбрать баскетбольную команду из пяти человек?

Решение. Так как из 25 человек выбираются 5 и порядок не важен, то число способов есть число сочетаний из 25 по 5, то есть:

Ответ: из группы в 25 человек можно выбрать баскетбольную команду 53130 способами.

НЕУПОРЯДОЧЕННЫЕ УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ С ФИКСИРОВАННЫМИ РАЗМЕРАМИ ЧАСТЕЙ

Цель: Изучить на практике методику расчета числа перестановок без повторений и с повторениями

Задание 4 () .

Задание 5 (начисло перестановок с повторениями).

Задание 6 (начисло неупорядоченных разбиений с фиксированными размерами частей) .

Задание 7 () .

Задание 4 (начисло перестановок без повторений) .

Сколько различных n n штук цифр: 1,3,5,7,9?

ЧИСЛО ПЕРЕСТАНОВОК БЕЗ ПОВТОРЕНИЙ. КРАТКАЯ ТЕОРИЯ

Перестановками без повторений или просто перестановками из элементов п различных типов называются их последовательности, отличающиеся друг от друга только порядком входящих в них элементов. (Здесь и дальше под последовательностью из п элементов понимается их линейно упорядоченное множество, аналогичное п книгам, стоящим в ряд на полке.)

Пример. Перестановки из 3 различных элементов а, b и с: аbс, bса, саb, сbа, bас, асb.

Число всех перестановок из п различных элементов (обозначается Р п) есть Р п = 1 2 3 ... n = п ! (п ! читается "эн-факториал").

В таблице ниже приведены числовые значения факториалов первых натуральных чисел и нуля.

Таблица. Значения факториалов первых натуральных чисел и нуля.

n=
n!=

КОНЕЦ ТЕОРИИ.

Решение.

В задании 4 n =5, ибо переставляются местами всевозможными способами n =5 штук различных цифр: 1,3,5,7,9. При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок без повторений из n =5 штук различных элементов.

Согласно теории, искомое число равно Р 5 = 5!= 120 различных 5– значных телефонных номеров.

Ответ: 120 различных 5– значных телефонных номеров.

Задание 5 (на число перестановок с повторениями.)

Сколько различных n – значных телефонных номеров (натуральных чисел) можно написать, переставляя следующий набор n штук цифр: 1,1,1,3,3,5?

ЧИСЛО ПЕРЕСТАНОВОК С ПОВТОРЕНИЯМИ. КРАТКАЯ ТЕОРИЯ

Перестановки с повторениями

Перестановками с повторениями из т элементов n различных типов, среди которых k 1 одинаковых элементов 1-го типа, k 2 одинаковых элементов 2-го типа, ... , k n одинаковых элементов п -го типа (k 1 + k 2 + ... + k п = m ) , называются их последовательности, отличающиеся только порядком входящих в них элементов.

Пример. Перестановки из 3 элементов, среди которых 2 одинаковых элемента типа а и 1 элемент типа b: ааb, аbа, bаа.

Число перестановок из т элементов, среди которых k 1 - одинаковых элементов 1-го типа, k 2 одинаковых элементов2-го типа,..., k п - одинаковых элементов n -го типа [обозначается Р (m ; k 1 ,k 2 ,..., k п) ] равно:

Р (m ; k 1 ,k 2 ,..., k п) = т!/ (k 1 !k 2 !... k п !).

Для примера перестановок с повторениями из 3 элементов, среди которых 2 одинаковых типа а и 1 элемент типа b, имеем Р (m=3 ; k 1 =2,k 2 =1) = 3!/ (2 !1!).

КОНЕЦ ТЕОРИИ.

Решение.

В задание 5 m =6, ибо переставляются местами всевозможными способами m =6 штук различных цифр: 1,1,1,3,3,5, среди которых есть повторяющиеся (одинаковые). При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок с повторениями из m =6 штук элементов, среди которых k 1 =3 одинаковых элементов 1-го типа (цифра 1), k 2 =2 одинаковых элементов2-го типа (цифра 3), k 3 =1одинаковых элементов 3 -го типа (цифра 5), равно Р (m ; k 1 ,k 2 ,..., k п) = т!/ (k 1 !k 2 !... k п !), Р (6; 3, 2, 1) = 6!/(3! 2! 1!)= =60.

Ответ: Р (6; 3, 2, 1) = 60, т. е 60 различных вариантов 6– значных телефонных номеров (6-значных чисел), содержащих цифру 1 трижды, 3 -дважды и 5 - один раз.

Задание 6 (на число неупорядоченных разбиений с фиксированными размерами частей) .

Сколько всего вариантов можно получить, разбивая группу из пяти человек (из пяти солдат) на три подгруппы - две подгруппы по два человека (по два автоматчики) и одна подгруппа из одного человека (из одного пулеметчика)?

НЕУПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ

Неупорядоченное разбиение n -элементного множества X - это любое семейство {X 1 , X 2 ,…, X k }, где 1≤k≤п; X 1 , X 2 ,…, X k - непустые попарно непересекающиеся подмножества множества X , объединение которых равноX.

Называем такое разбиение неупорядоченным, так как семейство - это неупорядоченная совокупность.

Пример. Для множества {а,b,с} неупорядоченное разбиение это, например, {{а},{b,с}}. Причем {{а},{b,с}}={{b,с},{а}}.

Для множества с п элементами обозначим через D (n ; k 1 , k 2 ,…, k n) число всех таких неупорядоченных разбиений, в которых есть k 1 подмножеств с одним элементом, k 2 подмножеств с двумя элементами и т.д., где k 1 ≥0, k 2 ≥0,…, k n ≥0; k 1 +2 k 2 +…+n k n = n.

КОНЕЦ ТЕОРИИ.

Решение.

Каждый вариант- это неупорядоченное разбиение { Иванов, Петров, Сидоров, Андреев, Борисов }. Множество из 5 элементов Один из вариантов разбиения {{Иванов, Петров}, {Сидоров, Андреев}, {Борисов}}

Имеем п = 5, k 1 =1, k 2 =2, k 3 =0, k 4 =0, k 5 =0 (так как по условию нет подгрупп из трех, четырех, пяти человек).

Ответ: 15 вариантов.

Задание 7 (начисло упорядоченных разбиений с фиксированными размерами частей) .

Сколькими способами можно выбрать из десяти солдат трех пулеметчиков, трех гранатометчиков и четырех автоматчиков (3 пулеметчика 3 гранатометчика 4 автоматчика, всего 10 солдат)?

УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ

Упорядоченным разбиением конечного множества X с n элементами называется любой кортеж вида <X 1 , X 2 ,…, X k >, где 1 ≤k ≤n ; X 1 , X 2 ,…, X k - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X.

Называем такое разбиение упорядоченным , так как элементы кортежа упорядочены.

Пример. Для множества {а,b,с} упорядоченное разбиение это, например, кортеж <{{а},{b,с}} >. Причем <{{а},{b,с}}> ¹<{{b,с},{а}} >.

Для множества с п элементами обозначим через E (n ; m 1 , m 2 ,…, m k ,) число всех таких упорядоченных разбиений на подмножества X 1 , X 2 ,…, X k , содержащие m 1 , m 2 ,…, m k , где m 1 ≥0, m 2 ≥0,…, m k ≥0; m 1 + m 2 +…+ m k = n.

Число всех упорядоченных разбиений <X 1 , X 2 ,…, X k > множества с п элементами на подмножества X 1 , X 2 ,…, X k , содержащие m 1 , m 2 ,…, m k , элементов соответственно. определяется по полиномиальной формуле

где m 1 ≥1, m 2 ≥1,…, m n ≥1; m 1 + m 2 +…+m k = n.

КОНЕЦ ТЕОРИИ.

Решение.

В задании имеем упорядоченное разбиение < X 1 , X 2 , X 3 > множества с десятью элементами, где X 1 - подмножество пулеметчиков, Х 2 - подмножество гранатометчиков, Х 3 - подмножество автоматчиков;

поэтому п = 10, m 1 = 3, т 2 , = 3, т 3 = 4.

Тогда всего есть

Ответ: 4200 вариантов

В этом разделе будут рассмотрены три вида соединений без повторений: размещения, перестановки и сочетания. Ради краткости добавку «без повторений» будем опускать.

1. Размещения. Размещения из n элементов по – это упорядоченные наборы из попарно различных элементов -множества . Таким образом, два размещения из элементов по различаются либо порядком, либо составом входящих в них элементов. Например, размещения из 3-множества по 2 исчерпываются следующими упорядоченными парами:

, , , , , .

Нас будет интересовать задача нахождения числа всех размещений из элементов по . В качестве первого элемента можно выбрать любой из элементов множества . После того как выбран первый элемент, второй элемент можно выбрать лишь способами (можно взять любой элемент, исключая выбранный). После выбора первых двух элементов остаются лишь возможности выбрать третий элемент и т. д. Последний -й элемент можно выбрать способами – ведь до него уже выбраны элемент, а потому осталось лишь элементов. По правилу произведения получаем, что число всевозможных упорядоченных наборов равно произведению чисел , , , …, , т.е. справедлива следующая

Т е о р е м а 1. Число размещений из элементов по находится по формуле

Напомним, что произведение первых n натуральных чисел, т.е. , называют n-факториалом и обозначают . Произведение можно записать в виде дроби = и поэтому формулу (1) можно переписать следующим образом

В частности, при из формулы (2) получаем

Это означает, что существует единственный упорядоченный набор длины 0 – пустой кортеж, не имеющий ни одной компоненты.

Пример 1. Найти число пятизначных чисел в десятичной системе счисления, в записи которых цифры не повторяются.

□ Рассуждая по аналогии с тем, как это делалось при рассмотрении примера 1 (2-й способ) из § 2, приходим к выводу, что искомое число есть .

2. Перестановки. Рассмотримтеперь различные линейные упорядочения данного -множества . Получаемые при этом упорядоченные наборы отличаются друг от друга лишь порядком входящих в них элементов. Их называют перестановками (без повторений) из n элементов, а их число обозначают через . Например, если , то = 6, так как из трех элементов можно составить шесть перестановок:

, , , , , .

Общая формула для получается из формулы (1), поскольку перестановка из элементов – это то же самое, что размещение без повторений из элементов по . Полагая в (1) получим = = = = . Итак, справедлива

Т е о р е м а 2. Число перестановок из элементов равно -факториал, т.е.

Полагая в формуле (2) , получаем

Сравнивая (3) и (4), приходим к выводу, что 0! = 1. На первый взгляд это равенство кажется парадоксальным. Но для всех справедливо равенство = . Если потребовать, чтобы это равенство было справедливо и при , то получим . Отсюда вновь следует, что естественно положить0! = 1 .

Пример 2. Сколькимиспособамиможно расположить на полке 7 различных учебников так, чтобы «Алгебра» и «Геометрия» не стояли рядом?

□ Условимся указанные учебники обозначать для краткости буквами А и Г соответственно. Число всевозможных способов расстановки учебников равно числу перестановок из семи элементов, т.е. . Но при этом сосчитаны и те, в которых встречаются рядом учебники А и Г, причем в двух позициях: АГ и ГА. Считая АГ и ГА за одну книгу, для каждого такого расположения получим расстановок, в которых учебники А и Г встречаются рядом. Искомое число расстановок учебников равно .

3. Сочетания. Одной из важнейших задач комбинаторики является подсчет числа k -подмножеств данного n -множества . Такие неупорядоченные подмножества называются сочетаниями из элементов по , а их число обозначают через (от французского слова combinaison – сочетание). Например, из элементов 4-множества можно составить следующие 2-множества: , , , , , . Число этих подмножеств равно 6. Следовательно, = 6. Отметим, что = 1, так как каждое множество имеет лишь одно 0-множество, а именно, пустое множество . Далее понятно, что = , поскольку в ‑множества содержится одноэлементных подмножеств. Ясно также, что .

Выведем формулу, выражающую через и . Для этого укажем способ получения всех размещений из элементов по . Выберем любое k -подмножество данного n -множества . Это можно сделать способами. Каждое такое k -подмножество упорядочим всевозможными способами. Таких различных упорядочений столько, сколько можно составить перестановок из элементов, т.е. = . Понятно, что таким способом получатся все размещений из элементов по . Значит, имеет место равенство = . Отсюда вытекает справедливость следующего утверждения.

Т е о р е м а 3. Число сочетаний из n элементов по k вычисляется по формуле :

= = = . (5)

Пример 3. Найти число всех диагоналей правильного n -угольника.

□ Любые две вершины n -угольника однозначно определяют отрезок, соединяющие эти вершины. Поэтому число всевозможных отрезков, соединяющих вершины n -угольника, равно числу сочетаний из по 2, т.е. . Но среди них находятся и сторон n -угольника, которые диагоналями не являются,

Таким образом, искомое число равно

.

Например, при получаем, что правильный 10-угольник имеет = 35 диагоналей.

Свойства сочетаний.

□ В самом деле, в силу формулы (5) имеем

= = = .

□ Действительно,

= = = . =

Непосредственно свойств ‑ сочетаний вытекают следующие

Число размещений без повторений из n по k n k различными координатами.

Число размещений без повторений находится по формуле:

Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?

Количество цифр
, размерность вектора с различными координатами

Число размещений с повторениями

Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.

Число размещений с повторениями находится по формуле:

.

Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?

Количество букв
, размерность вектора

Число перестановок без повторений

Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.

Число перестановок без повторений находится по формуле:

.

Замечание: Мощность искомого множества А удобно искать по формуле:
, гдех – число способов выбрать нужные места; у – число способов расположить на них нужные элементы; z – число способов расположить остальные элементы на оставшихся местах.

Пример. Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?

Всего способов расставить 5 книг на 5-ти местах – равно = 5! = 120.

В задаче х – число способов выбрать два места рядом, х = 4; у – число способов расположить две книги на двух местах, у = 2! = 2; z – число способов расположить остальные 3 книги на оставшихся 3-х местах, z = 3! = 6. Значит
= 48.

Число сочетаний без повторений

Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.

Число сочетаний без повторений находится по формуле:

.

Свойства:

1)
; 2)
; 3)
;

4)
; 5)
; 6)
.

Пример. В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет ровно один белый.

Всего способов
. Чтобы получить число способов выбрать 1 белый шар (из 3-х белых) и 2 черных шара (из 4-х черных), надо перемножить
и
Таким образом искомое количество способов

Упражнения

1. Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек. Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?

2. В группе из 30 студентов каждый знает, по крайней мере, один иностранный язык – английский или немецкий. Английский знают 22 студента, немецкий – 17. Сколько студентов знают оба языка? Сколько студентов знают немецкий язык, но не знают английский?

3. В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Америки. Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы; в 3 – и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты: 1) только с одного континента; 2) только с двух континентов; 3) только африканцы.

4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике и астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30 студентов, по математике и астрономии – 25; спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?

5. Староста курса представил следующий отчет по физкультурной работе. Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек. При этом, 16 человек одновременно посещают футбольную и баскетбольную секции, 18 – футбольную и шахматную, 17 – баскетбольную и шахматную, 15 человек посещают все три секции. Объясните, почему отчет не был принят.

6. В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: 1) ровно одна красная; 2) ровно 2 золотых; 3) хотя бы одна красная.

7. В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?

8. Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: 1) все карты были разных мастей; 2) все карты были одной масти; 3) 2 красные и 2 черные.

9. На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось «кукареку».

10. Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово «отолоринголог».

11. Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово «литература».

12. 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: 1) рядом; 2) на краях очереди;

13. 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: 1) два определенных человека А и Б; 2) три определенных человека А, Б и С.

14. Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: 1) все цифры были разными; 2) на последнем месте четная цифра.

15. Из 26 букв латинского алфавита (среди них 6 гласных) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: 1) ровно одна буква «а»; 2) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.

16. Сколько четырехзначных чисел делятся на 5?

17. Сколько четырехзначных чисел с различными цифрами делятся на 25?

19. Брошены 3 игральные кости. В скольких случаях выпала: 1) ровно 1 «шестерка»; 2) хотя бы одна «шестерка».

20. Брошены 3 игральные кости. В скольких случаях будет: 1) все разные; 2) ровно два одинаковых числа очков.

21. Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….