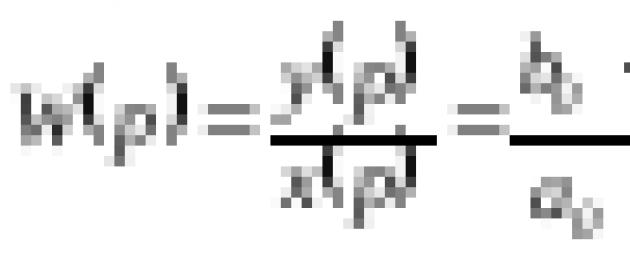Необходимое и достаточное условие устойчивости сау. Устойчивость системы автоматического управления. Высшего профессионального образования

Устойчивость САУ, общие понятия устойчивости

Наименование параметра	Значение
Тема статьи:	Устойчивость САУ, общие понятия устойчивости
Рубрика (тематическая категория)	Математика

Устойчивость системы автоматического управления является одной из важнейших характеристик системы, т.к. от нее зависит работоспособность системы. Система, у которой отсутствует устойчивость, не может качественно решать задачу управления. Отсутствие устойчивости также может привести к разрушению самой системы в процессе управления или разрушению объекта управления, в связи с этим использование неустойчивых систем нецелесообразно.

Устойчивость системы автоматического управления - это свойство системы воз-

вращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему состояния первоначального равновесия.

Примером устойчивых и неустойчивых систем могут служить системы из шарика, расположенного на вогнутой и выпуклой поверхности, представленные на рисунке 60.

Рис.60. Примеры систем: а) устойчивой; б) неустойчивой

На рисунке 60а шарик, расположенный на вогнутой поверхности и смещенный в сторону определенным усилием, после окончания внешнего воздействия возвратится в положение первоначального равновесия. При отсутствии трения о поверхность или его минимальном значении шарик будет совершать непродолжительные колебания около положения равновесия до возвращения в первоначальное положение равновесия (кривая 1- затухающий колебательный процесс). При большом трении шарик возвратится в положение первоначального равновесия без колебаний (кривая 2 - апериодический процесс). При очень большом значении трения шарик может не вернуться в положение первоначального равновесия (кривая 3), но возвратится в область, близкую к положению равновесия. В рассмотренном случае налицо наличие устойчивой системы. В устойчивых САУ возникают подобные переходные процессы (затухающие колебательные и апериодические).

На рисунке 60б шарик, расположенный на выпуклой поверхности и смещенный в сторону определенным усилием, не возвратится в положение первоначального равновесия (кривая 4), в связи с этим система является неустойчивой. В неустойчивых системах возникают переходные процессы виде расходящихся колебаний (кривая 5) или апериодические (кривая 4).

Неустойчивость САУ, как правило, возникает из-за очень сильного действия обратной связи. Причинами динамической неустойчивости обычно являются значительные инерционные характеристики звеньев замкнутой системы, из-за которых сигнал обратной связи в режиме колебаний так отстает от входного сигнала, что оказывается с ним в фазе. Получается, что характер действия отрицательной обратной связи приобретает характер

положительной.

Составим математическое описание устойчивости и неустойчивости. Так как устойчивость системы зависит только от характера ее свободного движения, то данное свободное движение системы можно описать однородным дифференциальным уравнением:

характеристическое уравнение, которого будет представлено следующим выражением:

Общее решение однородного дифференциального уравнения (2.19.) представим в следующем виде:

где C k – постоянные, зависящие от начальных условий, p k – корни характеристического уравнения.

Корни характеристического уравнения бывают комплексными (p k = α k ± jβ k ), действительными (p k = α k ) или мнимыми (p k = jβ k ). Комплексные корни всегда попарно сопряжены между собой, ᴛ.ᴇ. если имеется корень уравнения с положительной мнимой частью, то обязательно будет существовать корень с такой же по модулю, но отрицательной мнимой частью. y(t) при t → ∞ из (2.21.) будет стремиться к нулю лишь тогда, когда каждое слагаемое С к е p k t → 0. Характер данной функции будет зависеть от вида корня. Возможные случаи расположения корней p k на комплексной плоскости и соответствующие им функции y(t) = С к е p k t представлены на рисунке 61. Вид функций показан внутри эллипсов.

Рис.61. Влияние расположения корней характеристического уравнения на

составляющие свободного движения системы

На рисунке 61 видно, что если каждому действительному корню p k = α k для выражения (2.21.) будет соответствовать слагаемое:

y к (t) = С к е α k t (2.22.)

тогда приα к < 0 (корень p 1) функция при t → ∞ будет стремиться к нулю, при α к > 0 (корень p 3 ) функция будет неограниченно возрастать, а при α к = 0 (корень p 2)функция будет оставаться постоянной.

В случае если характеристическое уравнение будет иметь комплексные корни, то каждой паре сопряженных комплексных корней p k, k+1 = α k ± jβ k , будут соответствовать два слагаемых, которые можно объединить и представить в виде следующего выражения:

Данная функция представляет собой синусоиду с изменяющейся по экспоненте амплитудой и частотой β k . При отрицательной действительной части двух комплексных корней α к, к+1 < 0 , (корни p 4 и p 5 )колебательная составляющая функции будет затухать, а при положительной действительной части α к, к+1 > 0 , (корни p 8 и p 9 ) амплитуда колебаний будет увеличиваться неограниченно. При отсутствии действительной части комплексных корней α к, к+1 = 0 (корни p 6 и p 7 ), ᴛ.ᴇ. наличии только мнимых корней, функция будет представлять собой незатухающую синусоиду с частотой β k .

Исходя из определения устойчивости, в случае если первоначальное положение равновесия принимается за ноль, то у устойчивых систем величина выходного параметра с течением времени должна стремиться к нулю, ᴛ.ᴇ. система сама возвратится в положение равновесия. Необходимым и достаточным условием этого является, чтобы все слагаемые решения дифференциального уравнения (2.21.) с течением времени стремились к нулю, что должна быть достигнуто при отрицательных действительных корнях уравнения, а комплексные корни должны иметь отрицательную действительную часть. Существование хотя бы одного положительного действительного корня или пары комплексных корней с положительной действительной частью приведет к тому, что величина выходного параметра системы не возвратится к первоначальному значению, ᴛ.ᴇ. система будет неустойчивой.

Анализируя местоположение корней характеристического уравнения на комплексной плоскости, представленное на рисунке 62, можно заметить, что САУ является устойчивой, в случае если все корни характеристического уравнения находятся в левой полуплоскости и все они являются действительными отрицательными или комплексными с отрицательной действительной частью. Наличие хотя бы одного корня в правой полуплоскости будет характеризовать неустойчивость системы.

Устойчивость системы является внутренним свойством системы, зависящим только от вида корней характеристического уравнения, описывающего свойства системы, и не зависящим от внешнего воздействия. Необходимым и достаточным условием устойчивости системы является положение всех корней уравнения в левой (отрицательной) полуплоскости.

Положительную и отрицательную полуплоскости, в которых находятся положительные или отрицательные корни характеристического уравнения, обеспечивающие устойчивость или неустойчивость системы, разделяет мнимая ось ± jβ . Данная ось является границей устойчивости, в связи с этим если у характеристического уравнения есть одна пара чисто мнимых корней p k, k+1 =± jβ k , а другие корни находятсяв отрицательной полуплоскости, то система характеризуется наличием незатухающих колебаний с частотой ω = β к. Принято считать, что в таком случае система находится на колебательной границе устойчивости .

Точка β = 0 на мнимой оси соответствует нулевому корню. Считается, что уравнение, имеющее один нулевой корень, находится на апериодической границе устойчивости , а при наличии двух нулевых корней система неустойчива.

Рис.62. Расположение корней характеристического уравнения устойчивой системы на

комплексной плоскости

Не стоит забывать, что уравнения почти всех реальных САУ не являются линейными, а приведены к линейным уравнениям с помощью линеаризации, в связи с этим допущения, сделанные при линеаризации, могут повлиять на правильность определения устойчивости системы.

А. М. Ляпунов в 1892 ᴦ. в своей работе ʼʼОбщая задача об устойчивости движенияʼʼ привел доказательство теоремы, в которой были сделаны следующие выводы для линеаризованных уравнений:

1. В случае если все действительные корни характеристического уравнения системы являются отрицательными, то система считается устойчивой.

2. В случае если хотя бы один действительный корень характеристического уравнения системы положительный, то система считается неустойчивой.

3. В случае если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то нельзя судить об устойчивости реальной системы по линеаризованному уравнению.

Следовательно, вывод об устойчивости реальных систем крайне важно делать на базе анализа исходного нелинейного уравнения и для определения неустойчивости или устойчивости системы будет достаточно выявить положительность (отрицательность) действительных корней характеристического уравнения.

Критериями устойчивости называют определенные правила, по которым в теории автоматического управления определяют знаки корней характеристического уравнения, не решая его. Различают алгебраические и частотные критерии устойчивости.

Алгебраическими критериями устойчивости системыназывают крайне важно е и достаточное условие отрицательности корней при определенных значениях коэффициентов в характеристическом уравнении.

Частотными критериями устойчивости системы установлена зависимость устойчивости системы от формы частотных характеристик системы.

Устойчивость САУ, общие понятия устойчивости - понятие и виды. Классификация и особенности категории "Устойчивость САУ, общие понятия устойчивости" 2017, 2018.

САУ называется устойчивой, если при t  переходный процесс стремится к установившемуся значению. Учитывая то, что в линейных САУ по существу рассматриваются линеаризованные системы, то указанный вид устойчивости справедлив при малых отклонениях от первоначального устойчивого состояния. Эту устойчивость называют также "устойчивостью в малом". Иллюстрации такой устойчивости приведены на рис.1.33.

Свойство устойчивости для САУ является обязательным, так как неустойчивая САУ фактически неработоспособна.

Устойчивость можно оценить прямыми методами или при помощи критериев устойчивости.

Прямые методы оценки устойчивости.

Свойство устойчивости может быть определено по графику переходного процесса (рис.1.33г). Однако расчёт и построение графика переходного процесса требует больших вычислений.

Проще установить устойчивость без построения графика h (t ), а только по корням характеристического уравнения изображения переходного процесса h (p ). Каждому корню характеристического уравнения соответствует свой член, входящий как слагаемое в выражение h (t ) переходного процесса. В таблице 1.5 приведены соответствия корней характеристического уравнения САУ, вид слагаемых в выражении переходного процесса и характеристики устойчивости САУ.

Оценка устойчивости либо по графику переходного процесса, либо по корням характеристического уравнения имеет тот недостаток, что её невозможно в общем случае применить к САУ, в передаточной функции которой содержится хотя бы один буквенный коэффициент, так как не существует аналитических методов решения алгебраических уравнений (именно таким уравнением является характеристическое уравнение САУ) выше 3-й степени. По этой же причине неприменима указанная оценка устойчивости на этапе синтеза САУ.

Оценка устойчивости при помощи критериев устойчивости.

В ТАУ для оценки устойчивости применяются критерии устойчивости. Критериями устойчивости называются совокупность процедур и правил, с помощью которых можно установить факт устойчивости САУ без нахождения корней характеристического уравнения. Существуют различные виды таких критериев как алгебраических, так и частотных. Ниже рассмотрены наиболее применимые в ТАУ критерии Гурвица, Михайлова и Найквиста.

Таблица 1.5

Тип корня характеристического уравнения	Слагаемое в выражении h (t )	Переходный процесс h (t )
1. p =0		Устойчив
2. p 1 =0, p 2 =0 (два нулевых корня)	С  t	Неустойчив
3. p =  (действительный корень)		Устойчив при  <0 и неустойчив при  >0
4. p =  j  (комплексные корни)		Устойчив при  <0 и неустойчив при  >0
5. p =  j  (корни чисто мнимые)		На грани устойчивости

Критерий устойчивости Гурвица

Критерий Гурвица является алгебраическим. Для оценки устойчивости используется характеристический многочлен передаточной функции замкнутой САУ. Структура САУ может быть любой.

Вводная часть к критерию Гурвица.

Пусть замкнутая САУ имеет следующую передаточную функцию

Из коэффициентов характеристического многочлена

составляем следующую матрицу

Порядок заполнения матрицы следующий. Сначала по диагонали матрицы располагают коэффициенты от a 1 до a n . Затем над диагональными элементами располагают коэффициенты с возрастающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0. Далее под диагональными элементами располагают коэффициенты с убывающими индексами. Если коэффициенты в процессе заполнения все исчерпаны, то ставят 0.

Формулировка критерия Гурвица: САУ устойчива, если:

1) положительны все коэффициенты характеристического многочлена;

2) положительны все n главных (диагональных) определителей Гурвица матрицы (1.45):

(1.46)

Последний определитель не вычисляют, так как его знак совпадает со знаком Δ n -1 :

Δ n =a n  Δ n-1

Если хотя бы один определитель Гурвица отрицателен, то САУ неустойчива. Если имеется хотя бы один определитель Гурвица равен нулю при остальных положительных, то САУ находится на границе устойчивости.

Числовой пример.

Определить устойчивость САУ с передаточной функцией

Составляем матрицу Гурвица и главные определители

Оба определителя положительны, поэтому САУ устойчива.

Определение допустимых настроек САУ.

Если передаточная функция САУ содержит хотя бы один буквенный коэффициент, значение которого может быть любым числом, то с помощью критерия Гурвица можно определить допустимые по условию устойчивости значения такого коэффициента. При двух буквенных коэффициентах возможно совместное определение допустимых значений таких коэффициентов и выделение областей устойчивости на плоскости этих коэффициентов. Покажем это на примере.

Пусть САУ управления курсом судна, представленная на рис.1.34, состоит из двух звеньев - авторулевого и судна. Передаточные функции авторулевого и судна имеют вид, соответственно,

Постоянная времени T судна зависит от загрузки судна и изменяется от 10 с при порожнем судне до 60 с при полностью загруженном. Параметром настройки авторулевого является коэффициент передачи K . Необходимо найти такие значения параметра K , при которых САУ устойчива при изменении загрузки судна.

Определяем передаточную функцию замкнутой САУ

(1.48)

Составляем матрицу Гурвица и вычисляем 2-й определитель:

(1.49)

С учётом положительности всех коэффициентов характеристического многочлена при условии (1.49) САУ будет устойчива при одновременном выполнении следующей системы неравенств

САУ будет находиться на границе устойчивости, если будет выполнено хотя бы одно из равенств

Каждое из равенств (1.51) является на плоскости T - K границей области устойчивости (рис.1.35). Штриховкой обозначены области устойчивости по отношению к линиям границы устойчивости. Общая область a 0 d для всех заштрихованных областей является областью устойчивости САУ.

Пусть при порожнем судне с Т порож установлен коэффициент передачи K 1 регулятора. Этот состояние САУ отмечено точкой 1 , лежащей в области устойчивости. Если после загрузки судна значение T увеличится до T груж , то при том же K 1 САУ в точке 2 будет неустойчива. Необходимо будет увеличить K до значения K 3 , чтобы система оказалась в точке 3 . Область, ограниченная ломаной линией abcd , будет областью устойчивости при любой загрузке судна.

Одной из важнейших характеристик АСУ является ее устойчивость.

Устойчивость САУ – свойство системы возвращаться в состояние равновесия после прекращения изменения воздействия, выведшего систему из этого состояния.

Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы.

Неустойчивая система не возвращается в состояние равновесия, а непрерывно удаляется от него. От устойчивости САУ зависит ее работоспособность. Система, не обладающая устойчивостью, вообще не способна выполнять функции управления и имеет нулевую или даже отрицательную эффективность. Неустойчивая система может привести управляемый объект в аварийное состояние. Поэтому проблема устойчивости систем является одной из центральных в теории автоматического управления.

Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

Если система описывается линейным дифференциальным уравнением, то ее устойчивость не зависит от величины возмущения. Линейная система, устойчивая при малых возмущениях, будет устойчива и при больших. нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших.

Проблема устойчивости обычно возникает в замкнутых системах из-за влияния обратной связи. Поэтому в дальнейшем устойчивость исследуется на примерах замкнутых систем, хотя методы исследования устойчивости универсальны.

Неустойчивость САУ возникает, как правило, из-за неправильного (положительного) или очень сильного действия главной обратной связи. В результате чего в систему в режиме гармонических колебаний непрерывно поступает (закачивается) энергия. Энергия системы увеличивается. Увеличиваются и связанные с ней режимные параметры, например, регулируемая величина. Такое явление в технике получило название резонанса.

Причинами неправильного действия главной обратной связи САУ являются:

Выполнение главной обратной связи САУ по ошибке положительной вместо отрицательной, что практически при любых параметрах делает систему неустойчивой.

Значительная инерционность элементов замкнутого контура САУ (например, объекта управления), из-за которой в режиме колебаний системы сигнал главной обратной связи (например, управляемая величина) значительно отстает от входного сигнала (например, задающего воздействия) и оказывается с ним в фазе. Это означает, что связь, выполненная конструктивно как отрицательная, в динамическом режиме (режиме гармонических колебаний) начинает на определенной частоте действовать как положительная. Это ведет к раскачиванию системы и нарушению ее устойчивости.

Общее (математическое) условие устойчивости

Согласно данному выше физическому определению устойчивость определяется характером движения системы, когда воздействия, выведшие ее из состояния равновесия, прекратили действовать или изменяться во времени. Такое движение системы называют свободным. Оно происходит за счет внутренней энергии самой системы и зависит только от ее свойств (параметров). Для линейной или линеаризованной САУ:

(1)

С математической точки зрения:

Система устойчива, если свободная составляющая x(t) переходного процесса с течением времени стремится к нулю.

Общее математическое условие устойчивости :

для устойчивости линейной САУ необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными (или чтобы все корни характеристического уравнения системы располагались в левой части комплексной плоскости).

Линейные уравнения вида (1), как правило, получаются в результате упрощений и линеаризации исходных нелинейных уравнений. Возникает вопрос: в какой мере оценка устойчивости по линеаризованному уравнению будет справедлива для реальной системы, и не окажут ли существенное влияние на результат анализа отброшенные при линеаризации члены разложения? Ответ на него был дан русским математиком А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Он сформулировал и доказал следующую теорему:

если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то судить об устойчивости реальной системы по линеаризованному уравнению нельзя . Отброшенные при линеаризации малые члены могут сделать систему неустойчивой, и поэтому устойчивость реальной системы необходимо оценивать по исходному нелинейному уравнению.

Понятие о качестве управления в ТАУ

Качество САУ – совокупность свойств, обеспечивающих эффективное функционирование системы в целом.

Качество управления САУ – совокупность свойств САУ, характеризующих точность поддержания управляемой величины на заданном уровне в установившихся и переходных режимах.

Точность

Назначение САУ заключается в поддержании равенства

Основной способ снижения ошибки в САУ ОС – увеличение коэффициента усиления регулятора.

Однако это не значит, что можно таким образом достичь любой желаемой точности. Здесь начинает сказываться одно из фундаментальных противоречий в рамках теории управления - противоречие между точностью системы и запасом устойчивости. При чрезмерном увеличении коэффициента усиления возможна потеря устойчивости замкнутой системы. Повышение точности всегда приводит к уменьшению запаса устойчивости по амплитуде.

Различают точность, рассматриваемую в переходном процессе - динамическая точность , и точность в установившемся режиме - статическая точность .

Статическая точность в следящей системе определяется при гармоническом входном воздействии с использованием передаточной функции по ошибке.

Задав допустимые границы точности по амплитуде и по фазе, получим область частот, где гарантируется данная точность - это полоса пропускания.

Динамическая точность относится к более сложным задачам анализа систем, т.к. требует изучения всего переходного процесса.

Точность САУ в переходном режиме оценивают при помощи прямых и косвенных показателей качества.

Прямые показатели качества определяют по графику переходного процесса, возникающего в системе при ступенчатом внешнем воздействии.

Косвенные показатели качества определяют по распределению корней характеристического уравнения или по частотным характеристикам системы.

Различают колебательный (1), апериодический (2) и монотонный (3) типовые переходные процессы:

Познакомимся с показателями качества переходного процесса, вызванного ступенчатым изменением задающего воздействия:

Перерегулирование σ - величина, равная отношению первого максимального отклонения управляемой величины x(t) от ее установившегося значения x(∞) к этому установившемуся значению:

Качество управления считается удовлетворительным, если перерегулирование не превышает 30…40%.

Степень затухания :

Интенсивность затухания колебаний в системе считается удовлетворительной, если ψ = 0,75…0,95.

Длительность переходного процесса (время регулирования) t п – интервал времени от момента приложения ступенчатого воздействия до момента, после которого отклонения управляемой величины x(t) от ее нового установившегося значения x(∞) становятся меньше некоторого заданного числа δ п, т. е. до момента, после которого выполняется условие

⎢ x(t) - x(∞) ⎢ ≤ δ п.

В промышленной автоматике величину δ п обычно принимают равной 5% от установившегося значения x(∞).

Колебательность N – число переходов управляемой величины x(t) через ее установившееся значение x(∞) за время переходного процесса t п .

Рассмотренные прямые показатели качества удобно использовать в тех случаях, когда график переходного процесса x(t) можно получить экспериментально в реальной САУ или путем моделирования системы на ЭВМ.

Рассмотренная выше устойчивость (совместно с критериями ее определения) не является единственным свойством систем автоматического управления. Системы характеризуются: запасом устойчивости, областями устойчивости, притяжения, качеством регулирования и другими характеристиками. Рассмотрим некоторые из них.

Структурная устойчивость (неустойчивость)

Это такое свойство замкнутой системы, при наличии которого она не может быть сделана устойчивой ни при каких изменениях параметров.

Пусть
. Годограф Найквиста для данной системы изображен на Рис.А. Устойчивость этой системы определяется значениями параметров и
. Рассматриваемая система является структурно устойчивой.

Пусть
. (Рис.В). Устойчивость также зависит от параметров и. Система структурно устойчива.

Пусть
. В любом случае (при любых значениях параметров) система будет неустойчива. То есть система является структурно неустойчивой.

В частном случае передаточная функция имеет вид
. При этом соответствующее характеристическое уравнение замкнутой системы: . Нарушен принцип перемежаемости корней и полюсов. Система неустойчива. Структурно неустойчива.

Система с передаточной функцией
- структурно неустойчива, так как для замкнутой системы, при этом коэффициенты
,
,
,
, - все положительны, но из условияследует, что
, откуда
, или
. То есть система неустойчива.

Система
также структурно устойчива. Здесь звено
- квазиапериодическое (статически неустойчиво). Характеристическое уравнение замкнутой системы. Откуда можно получить два граничных условия:
и
.

Для одноконтурных систем имеют место условия (Мейеров М.В.):

Пусть одноконтурная система состоит из:

- интегрирующих звеньев,

- неустойчивых звеньев,

- консервативных звеньев. Тогда при отсутствии в системе дифференцирующих звеньев она будет структурно устойчива в том случае, если

В случае многоконтурных систем соотношения Мейерова необходимо применять к каждому контуру, входящему в систему.

Запас устойчивости

Факт обнаружения устойчивости не дает уверенности в работоспособности системы.

Возможны неточности (погрешности), так как:

математическое описании системы идеализировано;

часто бывает произведена линеаризация звеньев;

неточность определения параметров;

изменение условий работы (по отношению к моделируемым).

Следовательно, необходим запас устойчивости.

При использовании критерия Гурвица запас определяется величиной предпоследнего минора:

Если
- запас устойчивости отсутствует;
- запас имеется.

Запас устойчивости в системе характеризует степень устойчивости.

Запас устойчивости и степень устойчивости можно определить по расположению корней характеристического уравнения и по частотных характеристикам системы.

Аналогично можно определить запас устойчивости по логарифмическим характеристикам L( ) и ( ) , применяемым при определении устойчивости по критерию Найквиста.

Область устойчивости

На практике проектировщиков систем автоматического управления интересует пространство (область, пределы, диапазон) параметров, при которых системы является устойчивой. Множество значений параметров, при которых система обладает свойством устойчивости, называется областью устойчивостисистемы.

Для определения областей устойчивости имеется несколько методик.

На основе алгебраического критерия устойчивости Гурвица;

Метод Д-разбиения;

Метод корневого годографа.

Область устойчивости по Гурвицу определяется с помощью использования равенств в условиях Гурвица вместо неравенств. Чаще всего определение границы искомой области может быть произведено при условии
. (Смотри пункт "Определение критического коэффициента усиления"). Отсюда определяется зависимость интересующего нас параметраот параметра. Получаемая зависимость()- граница области устойчивости системы.

В системах более высоких порядков возникает необходимость рассмотрения других миноров. При этом область устойчивости может сужаться.

Устойчивость системы автоматического управления является одной из важнейших характеристик системы, т.к. от нее зависит работоспособность системы. Система, у которой отсутствует устойчивость, не может качественно решать задачу управления. Отсутствие устойчивости также может привести к разрушению самой системы в процессе управления или разрушению объекта управления, поэтому использование неустойчивых систем нецелесообразно.

Устойчивость системы автоматического управления - это свойство системы воз-

Рис.60. Примеры систем: а) устойчивой; б) неустойчивой

На рисунке 60б шарик, расположенный на выпуклой поверхности и смещенный в сторону определенным усилием, не возвратится в положение первоначального равновесия (кривая 4), поэтому система является неустойчивой. В неустойчивых системах возникают переходные процессы виде расходящихся колебаний (кривая 5) или апериодические (кривая 4).

положительной.

характеристическое уравнение, которого будет представлено следующим выражением:

Общее решение однородного дифференциального уравнения (2.19.) представим в следующем виде:

где C k – постоянные, зависящие от начальных условий, p k – корни характеристического уравнения.

Корни характеристического уравнения могут быть комплексными (p k = α k ± jβ k ), действительными (p k = α k ) или мнимыми (p k = jβ k ). Комплексные корни всегда попарно сопряжены между собой, т.е. если имеется корень уравнения с положительной мнимой частью, то обязательно будет существовать корень с такой же по модулю, но отрицательной мнимой частью. y(t) при t → ∞ из (2.21.) будет стремиться к нулю лишь тогда, когда каждое слагаемое С к е p k t → 0. Характер данной функции будет зависеть от вида корня. Возможные случаи расположения корней p k на комплексной плоскости и соответствующие им функции y(t) = С к е p k t представлены на рисунке 61. Вид функций показан внутри эллипсов.

Рис.61. Влияние расположения корней характеристического уравнения на

составляющие свободного движения системы

y к (t) = С к е α k t (2.22.)

Если характеристическое уравнение будет иметь комплексные корни, то каждой паре сопряженных комплексных корней p k, k+1 = α k ± jβ k , будут соответствовать два слагаемых, которые можно объединить и представить в виде следующего выражения:

Данная функция представляет собой синусоиду с изменяющейся по экспоненте амплитудой и частотой β k . При отрицательной действительной части двух комплексных корней α к, к+1 < 0 , (корни p 4 и p 5 )колебательная составляющая функции будет затухать, а при положительной действительной части α к, к+1 > 0 , (корни p 8 и p 9 ) амплитуда колебаний будет увеличиваться неограниченно. При отсутствии действительной части комплексных корней α к, к+1 = 0 (корни p 6 и p 7 ), т.е. наличии только мнимых корней, функция будет представлять собой незатухающую синусоиду с частотой β k .

Исходя из определения устойчивости, если первоначальное положение равновесия принимается за ноль, то у устойчивых систем величина выходного параметра с течением времени должна стремиться к нулю, т.е. система сама возвратится в положение равновесия. Необходимым и достаточным условием этого является, чтобы все слагаемые решения дифференциального уравнения (2.21.) с течением времени стремились к нулю, что может быть достигнуто при отрицательных действительных корнях уравнения, а комплексные корни должны иметь отрицательную действительную часть. Существование хотя бы одного положительного действительного корня или пары комплексных корней с положительной действительной частью приведет к тому, что величина выходного параметра системы не возвратится к первоначальному значению, т.е. система будет неустойчивой.

Анализируя местоположение корней характеристического уравнения на комплексной плоскости, представленное на рисунке 62, можно заметить, что САУ является устойчивой, если все корни характеристического уравнения находятся в левой полуплоскости и все они являются действительными отрицательными или комплексными с отрицательной действительной частью. Наличие хотя бы одного корня в правой полуплоскости будет характеризовать неустойчивость системы.

Положительную и отрицательную полуплоскости, в которых находятся положительные или отрицательные корни характеристического уравнения, обеспечивающие устойчивость или неустойчивость системы, разделяет мнимая ось ± jβ . Данная ось является границей устойчивости, поэтому если у характеристического уравнения есть одна пара чисто мнимых корней p k, k+1 =± jβ k , а другие корни находятсяв отрицательной полуплоскости, то система характеризуется наличием незатухающих колебаний с частотой ω = β к. Принято считать, что в таком случае система находится на колебательной границе устойчивости .

Рис.62. Расположение корней характеристического уравнения устойчивой системы на

комплексной плоскости

Не стоит забывать, что уравнения почти всех реальных САУ не являются линейными, а приведены к линейным уравнениям с помощью линеаризации, поэтому допущения, сделанные при линеаризации, могут повлиять на правильность определения устойчивости системы.

А. М. Ляпунов в 1892 г. в своей работе «Общая задача об устойчивости движения» привел доказательство теоремы, в которой были сделаны следующие выводы для линеаризованных уравнений:

1. Если все действительные корни характеристического уравнения системы являются отрицательными, то система считается устойчивой.

2. Если хотя бы один действительный корень характеристического уравнения системы положительный, то система считается неустойчивой.

3. Если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то нельзя судить об устойчивости реальной системы по линеаризованному уравнению.

Следовательно, вывод об устойчивости реальных систем необходимо делать на основе анализа исходного нелинейного уравнения и для определения неустойчивости или устойчивости системы будет достаточно выявить положительность (отрицательность) действительных корней характеристического уравнения.

Алгебраическими критериями устойчивости системыназывают необходимое и достаточное условие отрицательности корней при определенных значениях коэффициентов в характеристическом уравнении.

Total: 0
Вконтакте0
Google+0
ОК0
Facebook0